
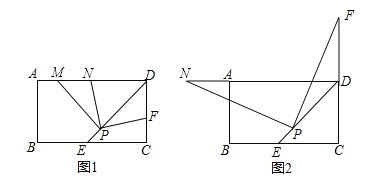
����Ŀ������ABCD�У�DEƽ�֡�ADC��BC���ڵ�E��PΪDE�ϵ�һ�㣨PE��PD����PM��PD��PM��AD���ڵ�M��
��1������F�DZ�CD��һ�㣬����PF��PN���ҵ�Nλ��AD���ϣ���ͼ1��ʾ��
��֤����PN=PF����DF+DN=![]() DP��
DP��
��2����ͼ2��ʾ������F��CD�ߵ��ӳ�����ʱ����Ȼ����PF��PN����ʱ��Nλ��DA�ߵ��ӳ����ϣ���ͼ2��ʾ������DF��DN��DP��������������ϵ��������֤����
���𰸡���1��֤����������2��![]()
����������������1�������þ��ε������������֪������֤��PMN�ա�PDF�����֤�ý��������ɹ��ɶ��������DM=![]() DP�����âٿ����MN=DF�����֤�ý�����
DP�����âٿ����MN=DF�����֤�ý�����
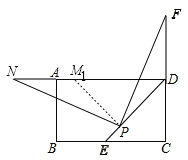
��2������P��PM1��PD��PM1��AD���ڵ�M1�����֤�á�PM1N�ա�PDF�����֤��M1N=DF��ͬ��1���ڵķ�����֤�ý��ۣ�
�������1���١��ı���ABCD�Ǿ��������ADC=90�㣮
�֡�DEƽ�֡�ADC�����ADE=��EDC=45�㣻
��PM��PD����DMP=45�㣬��DP=MP��
��PM��PD��PF��PN�����MPN+��NPD=��NPD+��DPF=90�㣬���MPN=��DPF��
����PMN�͡�PDF�У��� 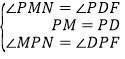 ��
��
���PMN�ա�PDF��ASA������PN=PF��MN=DF��
�ڡ�PM��PD��DP=MP����DM2=DP2+MP2=2DP2����DM=![]() DP��
DP��
���֡�DM=DN+MN�����ɢٿɵ�MN=DF����DM=DN+DF����DF+DN=![]() DP��
DP��
��2��![]() ������������
������������
����P��PM1��PD��PM1��AD���ڵ�M1����ͼ��
���ı���ABCD�Ǿ��������ADC=90�㣮
�֡�DEƽ�֡�ADC�����ADE=��EDC=45�㣻
��PM1��PD����DM1P=45�㣬��DP=M1P�����PDF=��PM1N=135�㣬ͬ��1����֪��M1PN=��DPF������PM1N�͡�PDF����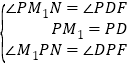 ��
��
���PM1N�ա�PDF��ASA������M1N=DF���ɹ��ɶ����ɵ���![]() =DP2+M1P2=2DP2����DM1
=DP2+M1P2=2DP2����DM1![]() DP��
DP��
��DM1=DN��M1N��M1N=DF����DM1=DN��DF����DN��DF=![]() DP��
DP��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1������ABCD�У���A=60�㣬��P��A��������2cm/s���ٶ��ر�AB��BC��CD�����˶���D��ֹ����Q��A��Pͬʱ�������ر�AD�����˶���D��ֹ�����P�˶���ʱ��Ϊt��s������APQ�����S��cm2����t��s��֮�亯����ϵ��ͼ����ͼ2�е����߶�OE���߶�EF��FG������
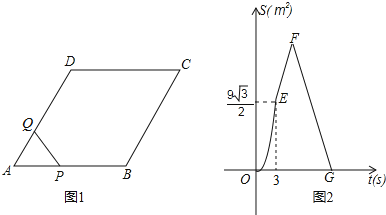
��1�����Q�˶����ٶȣ�
��2����ͼ2���߶�FG�ĺ�����ϵʽ��
��3���ʣ��Ƿ����������t��ʹPQ������ABCD�����ǡ�÷ֳ�1��5�������֣������ڣ����������t��ֵ���������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����λͬѧ��������仭ͼ����ϰ����ͬѧ����䡰ֱ�߾���A��B��C���㣬�ҵ�C�ڵ�A���B֮�䡱������ͼ�Σ�1������ͬѧ����䡰�����߶�AB��CD�ཻ�ڵ�P������ͼ�Σ�2������ͬѧ����䡰��P��ֱ��l�ϣ���Q��ֱ��l�⡱����ͼ�Σ�3������ͬѧ����䡰��M���߶�AB���ӳ����ϣ���N���߶�AB�ķ����ӳ����ϡ�����ͼ�Σ�4�������л��IJ���ȷ���ǣ�������

A. ��ͬѧB. ��ͬѧC. ��ͬѧD. ��ͬѧ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ����һ��5�����Ļ����ȣ�������ͼ��ʽ����߳�Ϊ1�������ε�ש��ͼ����Ӱ����Ϊ��ɫ��ש����ɫ����Ϊ��ͨ��ש��

��1��������ȳ�8�ף�����Ҫ��ɫ��ש�� ���飬��ͨ��ש�� ���飻
��2��������ȳ�2a�ף�aΪ��������������Ҫ��ɫ��ש�� ���飻
��3������ʱ��ǡ���ש�г���ש��������ɫ��שԭ��Ϊ100Ԫ/�飬��ͨ��שԭ��Ϊ40Ԫ/�飬�Żݷ���Ϊ����һ���ɫ��ש����һ����ͨ��ש��
��������ȳ�x�ף�xΪ���������ú�x����ʽ��ʾ�����ש�����Ǯ����
�ڵ�x��51��ʱ�������ש����Ǯ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����8����÷����ÿ��5ǧ��Ϊ����������ǧ�������������������ǧ���������������ƺ�ļ�¼���£�

�ش��������⣺
��1����8����÷�У���ӽ�5ǧ�˵��ǿ���÷Ϊ����ǧ�ˣ�
��2����ÿ��5ǧ��Ϊ������8����÷�ܼƳ�������ǧ�˻��߲������ǧ�ˣ�
��3������÷ÿǧ���ۼ�25Ԫ���������8����÷��������Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��1����2��Ҫ˵����ABD����ACD�����������������ѡһ���������ѡ���ǣ� ��
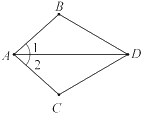
A. ��ADB����ADCB. ��B����CC. DB��DCD. AB��AC
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ֪��l![]() ����A��2��3��B��
����A��2��3��B��![]() ��0��
��0��
(1) ��ֱ��l![]() �Ľ���ʽ��l
�Ľ���ʽ��l![]() ��������Χ�ɵ�ͼ�ε����.
��������Χ�ɵ�ͼ�ε����.
(2) ��l![]() ����ƽ��3����λ���ȣ�������ƽ��1����λ���ȣ��õ�ֱ��l
����ƽ��3����λ���ȣ�������ƽ��1����λ���ȣ��õ�ֱ��l![]() ������l
������l![]() ��ͼ��ֱ��д��l
��ͼ��ֱ��д��l![]() �Ľ���ʽ__________________.
�Ľ���ʽ__________________.
(3)����M��![]() ��m����N��n��1����ֱ��l
��m����N��n��1����ֱ��l![]() �ϣ�PΪy����һ���㣬��PM+PN��Сʱ��P������Ϊ____________����ʱPM+PN=______________.
�ϣ�PΪy����һ���㣬��PM+PN��Сʱ��P������Ϊ____________����ʱPM+PN=______________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
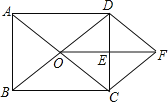
����Ŀ����֪����ͼ���ھ���ABCD�У��Խ���AC��BD�ཻ�ڵ�O��E��CD�е㣬����OE������C��CF��BD���߶�OE���ӳ����ڵ�F������DF����֤��
��1����ODE�ա�FCE��
��2���ı���ODFC�����Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������⡢̽�����ɣ�Ҫ��һ˫�����˫�ۣ������ͼ�����ɱ߳�Ϊ1��С�����ΰ���ij�ֹ������ж��ɵģ�

��1���۲�ͼ�Σ���д�±���
ͼ�θ�����n�� | ��1�� | ��2�� | ��3�� |
�����εĸ��� | 8 | �� �� | �� �� |
ͼ�ε��ܳ� | 18 | �� �� | �� �� |
��2���Ʋ��n��ͼ���У����������� �������ܳ�Ϊ�� ����
��3��д����30��ͼ�ε��ܳ���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com