
【题目】某校准备建一条5米宽的文化长廊,并按下图方式铺设边长为1米的正方形地砖,图中阴影部分为彩色地砖,白色部分为普通地砖.

(1)如果长廊长8米,则需要彩色地砖 块,普通地砖 块;
(2)如果长廊长2a米(a为正整数),则需要彩色地砖 块;
(3)购买时,恰逢地砖市场地砖促销,彩色地砖原价为100元/块,普通地砖原价为40元/块,优惠方案为:买一块彩色地砖赠送一块普通地砖.
①如果长廊长x米(x为整数),用含x代数式表示购买地砖所需的钱数;
②当x=51米时,求购买地砖所需钱数.
【答案】(1)12,28; (2)3a;(3)①当x为奇数时,购买地砖所需的钱数为230x+10;当x为偶数时,购买地砖所需的钱数为230元;②当x=51米时,购买地砖所需钱数为11740元.
【解析】
(1)观察图形,发现规律,计算得到结果;
(2)根据图形中彩色砖和普通砖的关系,得结果;
(3)①根据:所需钱数=彩砖钱数+普通砖钱数=彩砖数×彩砖单价+(需要总砖数-彩砖数)×普通砖单价,并对x的奇、偶进行讨论;
②把x=51代入①中代数式直接得结果.
解:(1)若长廊长8米,彩色砖需要3×![]() =12(块),
=12(块),
需要普通地砖2×8+3×![]() =28(块)或5×8﹣12=28(块);
=28(块)或5×8﹣12=28(块);
故答案为:12,28
(2)若长廊长2a米,彩色砖需要3×![]() =3a(块),
=3a(块),
故答案为:3a
(3)①当x为奇数时,购买地砖所需的钱数为:
![]() =230x+10
=230x+10
当x为偶数时,购买地砖所需的钱数为:![]()
②当x=51时,230x+10=11740元
答:当x=51米时,购买地砖所需钱数为11740元.


科目:初中数学 来源: 题型:
【题目】如图,PA为⊙O的切线,A为切点。过A作OP的垂线AB,垂足为点C,交⊙O于点B。延长BO与⊙O交于点D,与PA的延长线交于点E。
(1)求证:PB为⊙O的切线;
(2)试探究线段AD、AB、CP之间的等量关系,并加以证明。

查看答案和解析>>
科目:初中数学 来源: 题型:
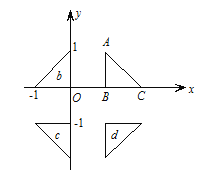
【题目】如图,等腰直角三角形![]() 分别沿着某条直线对称得到图形
分别沿着某条直线对称得到图形![]() .若上述对称关系保持不变,平移
.若上述对称关系保持不变,平移![]() ,使得四个图形能够围成一个不重叠且无缝隙的正方形,此时点
,使得四个图形能够围成一个不重叠且无缝隙的正方形,此时点![]() 的坐标和正方形的边长为( )
的坐标和正方形的边长为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,半径为1的小圆与半径为2的大圆上有一点与数轴上原点重合,两圆在数轴上做无滑动的滚动,小圆的运动速度为每秒π个单位,大圆的运动速度为每秒2π个单位.
(1)若大圆沿数轴向左滚动1周,则该圆与数轴重合的点所表示的数是 ;
(2)若小圆不动,大圆沿数轴来回滚动,规定大圆向右滚动时间记为正数,向左滚动时间记为负数,依次滚动的情况记录如下(单位:秒):﹣1,+2,﹣4,﹣2,+3,﹣8
①第几次滚动后,大圆离原点最远?
②当大圆结束运动时,大圆运动的路程共有多少?此时两圆与数轴重合的点之间的距离是多少?(结果保留π)
(3)若两圆同时在数轴上各自沿着某一方向连续滚动,滚动一段时间后两圆与数轴重合的点之间相距9π,求此时两圆与数轴重合的点所表示的数.

![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
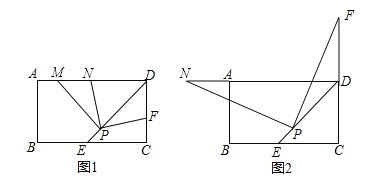
【题目】矩形ABCD中,DE平分∠ADC交BC边于点E,P为DE上的一点(PE<PD),PM⊥PD,PM交AD边于点M.
(1)若点F是边CD上一点,满足PF⊥PN,且点N位于AD边上,如图1所示.
求证:①PN=PF;②DF+DN=![]() DP;
DP;
(2)如图2所示,当点F在CD边的延长线上时,仍然满足PF⊥PN,此时点N位于DA边的延长线上,如图2所示;试问DF,DN,DP有怎样的数量关系,并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
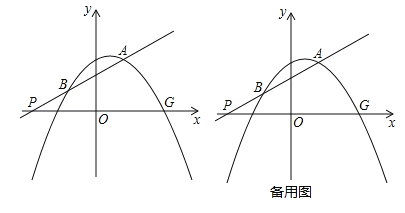
【题目】如图,二次函数y=﹣![]() x2+mx+n的图象经过点A(2,3),与x轴的正半轴交于点G(1+
x2+mx+n的图象经过点A(2,3),与x轴的正半轴交于点G(1+![]() ,0);一次函数y=kx+b的图象经过点A,且交x轴于点P,交抛物线于另一点B,又知点A,B位于点P的同侧.
,0);一次函数y=kx+b的图象经过点A,且交x轴于点P,交抛物线于另一点B,又知点A,B位于点P的同侧.
(1)求这个二次函数的解析式;
(2)若PA=3PB,求一次函数的解析式;
(3)在(2)的条件下,当k>0时,抛物线的对称轴上是否存在点C,使⊙C同时与x轴和直线AP都相切?如果存在,请求出点C的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一次函数y=k1x+b的图象分别与x轴、y轴的正半轴交于 A,B 两点,且与反比例函数y=![]() 交于 C,E 两点,点 C 在第二象限,过点 C 作CD⊥x轴于点 D,AC=2
交于 C,E 两点,点 C 在第二象限,过点 C 作CD⊥x轴于点 D,AC=2![]() ,OA=OB=1.
,OA=OB=1.

(1)△ADC 的面积;
(2)求反比例函数y= ![]() 与一次函数的y=k1x+b表达式.
与一次函数的y=k1x+b表达式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com