
【题目】如图,半径为1的小圆与半径为2的大圆上有一点与数轴上原点重合,两圆在数轴上做无滑动的滚动,小圆的运动速度为每秒π个单位,大圆的运动速度为每秒2π个单位.
(1)若大圆沿数轴向左滚动1周,则该圆与数轴重合的点所表示的数是 ;
(2)若小圆不动,大圆沿数轴来回滚动,规定大圆向右滚动时间记为正数,向左滚动时间记为负数,依次滚动的情况记录如下(单位:秒):﹣1,+2,﹣4,﹣2,+3,﹣8
①第几次滚动后,大圆离原点最远?
②当大圆结束运动时,大圆运动的路程共有多少?此时两圆与数轴重合的点之间的距离是多少?(结果保留π)
(3)若两圆同时在数轴上各自沿着某一方向连续滚动,滚动一段时间后两圆与数轴重合的点之间相距9π,求此时两圆与数轴重合的点所表示的数.

![]()
【答案】(1)﹣4π;
(2)①第6次滚动后,大圆离原点最远;
②当大圆结束运动时,大圆运动的路程共有40π,此时两圆与数轴重合的点之间的距离是20π;
(3)18π、9π或﹣18π、﹣9π或6π、﹣3π或﹣6π、3π.
【解析】
(1)该圆与数轴重合的点所表示的数的绝对值,就是大圆的周长;
(2)①分别计算出第几次滚动后,大圆离原点的距离,比较作答;
②先计算总路程,因为小圆不动,计算各数之和为-10,即大圆最后的落点为原点左侧,向左滚动10秒,距离为20π;
(3)分四种情况进行讨论:大圆和小圆分别在同侧,异侧时,表示出各自与数轴重合的点所表示的数.根据两圆与数轴重合的点之间相距9π列等式,求出即可.
解:(1)若大圆沿数轴向左滚动1周,则该圆与数轴重合的点所表示的数是﹣2π2=﹣4π;
(2)①第1次滚动后,|﹣1|=1,
第2次滚动后,|﹣1+2|=1,
第3次滚动后,|﹣1+2﹣4|=3,
第4次滚动后,|﹣1+2﹣4﹣2|=5,
第5次滚动后,|﹣1+2﹣4﹣2+3|=2,
第6次滚动后,|﹣1+2﹣4﹣2+3﹣8|=10,
则第6次滚动后,大圆离原点最远;
②1+2+4+3+2+8=20,
20×2π=40π,
﹣1+2﹣4﹣2+3﹣8=﹣10,
∴当大圆结束运动时,大圆运动的路程共有40π,此时两圆与数轴重合的点之间的距离是20π;
(3)设时间为t秒,
分四种情况讨论:
i)当两圆同向右滚动,
由题意得:t秒时,大圆与数轴重合的点所表示的数:2πt,
小圆与数轴重合的点所表示的数为:πt,
2πt﹣πt=9π,
2t﹣t=9,
t=9,
2πt=18π,πt=9π,
则此时两圆与数轴重合的点所表示的数分别为18π、9π.
ii)当两圆同向左滚动,
由题意得:t秒时,大圆与数轴重合的点所表示的数:﹣2πt,
小圆与数轴重合的点所表示的数:﹣πt,
﹣πt+2πt=9π,
﹣t+2t=9,
t=9,
﹣2πt=﹣18π,﹣πt=﹣9π,
则此时两圆与数轴重合的点所表示的数分别为﹣18π、﹣9π.
iii)当大圆向右滚动,小圆向左滚动时,
同理得:2πt﹣(﹣πt)=9π,
3t=9,
t=3,
2πt=6π,﹣πt=﹣3π,
则此时两圆与数轴重合的点所表示的数分别为6π、﹣3π.
iiii)当大圆向左滚动,小圆向右滚动时,
同理得:πt﹣(﹣2πt)=9π,
t=3,
πt=3π,﹣2πt=﹣6π,
则此时两圆与数轴重合的点所表示的数分别为﹣6π、3π.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】小学时候大家喜欢玩的幻方游戏,老师稍加创新改成了“幻圆”游戏,现在将﹣1、2、﹣3、4、﹣5、6、﹣7、8分别填入图中的圆圈内,使横、竖以及内外两圈上的4个数字之和都相等,老师已经帮助同学们完成了部分填空,则图中a+b的值为( )

A. ﹣6或﹣3 B. ﹣8或1 C. ﹣1或﹣4 D. 1或﹣1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A=﹣xy+x+1,B=4x+3y,
(1)当x=﹣2, y=0.6时,求A+2B的值;
(2)若代数式2A﹣B的结果与字母y的取值无关,求x的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校准备建一条5米宽的文化长廊,并按下图方式铺设边长为1米的正方形地砖,图中阴影部分为彩色地砖,白色部分为普通地砖.

(1)如果长廊长8米,则需要彩色地砖 块,普通地砖 块;
(2)如果长廊长2a米(a为正整数),则需要彩色地砖 块;
(3)购买时,恰逢地砖市场地砖促销,彩色地砖原价为100元/块,普通地砖原价为40元/块,优惠方案为:买一块彩色地砖赠送一块普通地砖.
①如果长廊长x米(x为整数),用含x代数式表示购买地砖所需的钱数;
②当x=51米时,求购买地砖所需钱数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() ,
,![]() 为
为![]() 内部的一条射线,
内部的一条射线,![]() .
.
(1)如图1,若![]() 平分
平分![]() ,
,![]() 为
为![]() 内部的一条射线,
内部的一条射线,![]() ,求
,求![]() 的度数;
的度数;

(2)如图2,若射线![]() 绕着
绕着![]() 点从
点从![]() 开始以每秒
开始以每秒![]() 的速度顺时针旋转至
的速度顺时针旋转至![]() 结束、
结束、![]() 绕着
绕着![]() 点从
点从![]() 开始以每秒
开始以每秒![]() 的速度逆时针旋转至
的速度逆时针旋转至![]() 结束,当一条射线到达终点时另一条射线也停止运动.若运动时间为
结束,当一条射线到达终点时另一条射线也停止运动.若运动时间为![]() 秒,当
秒,当![]() 时,求
时,求![]() 的值;
的值;

(3)若射线![]() 绕着
绕着![]() 点从
点从![]() 开始以每秒
开始以每秒![]() 的速度逆时针旋转至
的速度逆时针旋转至![]() 结束,在旋转过程中,
结束,在旋转过程中,![]() 平分
平分![]() ,试问
,试问![]() 在某时间段内是否为定值;若不是,请说明理由;若是,请补全图形,并直接写出这个定值以及
在某时间段内是否为定值;若不是,请说明理由;若是,请补全图形,并直接写出这个定值以及![]() 相应所在的时间段.(本题中的角均为大于
相应所在的时间段.(本题中的角均为大于![]() 且小于
且小于![]() 的角)
的角)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠1=∠2,要说明△ABD≌△ACD,还需从下列条件中选一个,错误的选法是( )
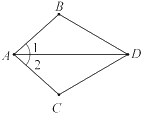
A. ∠ADB=∠ADCB. ∠B=∠CC. DB=DCD. AB=AC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】骰子是一种特别的数字立方体(见下图),它符合规则:相对两面的点数之和总是7,下面四幅图中可以折成符合规则的骰子的是( )
![]()
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com