
����Ŀ����֪![]() ��
��![]() Ϊ
Ϊ![]() �ڲ���һ�����ߣ�
�ڲ���һ�����ߣ�![]() .
.
��1����ͼ1����![]() ƽ��
ƽ��![]() ��
��![]() Ϊ
Ϊ![]() �ڲ���һ�����ߣ�
�ڲ���һ�����ߣ�![]() ����
����![]() �Ķ�����
�Ķ�����

��2����ͼ2��������![]() ����
����![]() ���
���![]() ��ʼ��ÿ��
��ʼ��ÿ��![]() ���ٶ�˳ʱ����ת��
���ٶ�˳ʱ����ת��![]() ������
������![]() ����
����![]() ���
���![]() ��ʼ��ÿ��
��ʼ��ÿ��![]() ���ٶ���ʱ����ת��
���ٶ���ʱ����ת��![]() ��������һ�����ߵ����յ�ʱ��һ������Ҳֹͣ�˶�.���˶�ʱ��Ϊ
��������һ�����ߵ����յ�ʱ��һ������Ҳֹͣ�˶�.���˶�ʱ��Ϊ![]() �룬��
�룬��![]() ʱ����
ʱ����![]() ��ֵ��
��ֵ��

��3��������![]() ����
����![]() ���
���![]() ��ʼ��ÿ��
��ʼ��ÿ��![]() ���ٶ���ʱ����ת��
���ٶ���ʱ����ת��![]() ����������ת�����У�
����������ת�����У�![]() ƽ��
ƽ��![]() ������
������![]() ��ijʱ������Ƿ�Ϊ��ֵ�������ǣ���˵�����ɣ����ǣ��벹ȫͼ�Σ���ֱ��д�������ֵ�Լ�
��ijʱ������Ƿ�Ϊ��ֵ�������ǣ���˵�����ɣ����ǣ��벹ȫͼ�Σ���ֱ��д�������ֵ�Լ�![]() ��Ӧ���ڵ�ʱ���.�������еĽǾ�Ϊ����
��Ӧ���ڵ�ʱ���.�������еĽǾ�Ϊ����![]() ��С��
��С��![]() �Ľǣ�
�Ľǣ�

���𰸡���1��![]() ����2��t��ֵΪ3��7.5����3����
����2��t��ֵΪ3��7.5����3����![]() ��
��![]() ʱ��
ʱ��![]() Ϊ��ֵ����ʱ��ȫ��ͼ�μ�������
Ϊ��ֵ����ʱ��ȫ��ͼ�μ�������
��������
��1���ȸ��ݽ�ƽ���ߵĶ������![]() �Ķ������ٸ��ݽǵı������
�Ķ������ٸ��ݽǵı������![]() �Ķ����������ݽǵĺͲ�ɣ�
�Ķ����������ݽǵĺͲ�ɣ�
��2�������![]() �Ķ�����t�����ֵ���Ӷ���ֹ֪ͣ�˶�ʱ��OF��OC���Ҳ࣬��ˣ���OE��OC�����Ҳ�����������ٸ���
�Ķ�����t�����ֵ���Ӷ���ֹ֪ͣ�˶�ʱ��OF��OC���Ҳ࣬��ˣ���OE��OC�����Ҳ�����������ٸ���![]() �г���ʽ��⼴�ɣ�
�г���ʽ��⼴�ɣ�
��3�������еĽǾ�Ϊ����![]() ��С��
��С��![]() �Ľǣ������OM��OB��һ��ֱ���ϡ�ON��OB��һ��ֱ���ϡ�OM��OA��һ��ֱ���������ٽ�λ�ã��Ӷ������ʱt��ȡֵ��Χ�����������Χ��
�Ľǣ������OM��OB��һ��ֱ���ϡ�ON��OB��һ��ֱ���ϡ�OM��OA��һ��ֱ���������ٽ�λ�ã��Ӷ������ʱt��ȡֵ��Χ�����������Χ��![]() ��
��![]() �Ķ��������ɵó��𰸣�
�Ķ��������ɵó��𰸣�
��1��![]() ƽ��
ƽ��![]() ��
��![]()
![]()
![]()
![]()
![]() ��
��
��2��![]()
![]()
������֪����OEת��OBʱ���������߾�ֹͣ�˶�
��ʱ![]() ���룩
���룩
��OFֹͣת��ʱ��![]()
��OF�ӿ�ʼ��ת��ֹͣ�˶���ʼ����OC���Ҳ�
��ˣ�������2�������
�ٵ�OE��OC���ʱ��![]()
����![]() ��
��![]() �����
�����![]()
�ڵ�OE��OC�Ҳ�ʱ��![]()
����![]() ��
��![]() �����
�����![]()
���ϣ�t��ֵΪ3��7.5��
��3������OM�ӿ�ʼת����OB����ʱ��ת��ʱ��Ϊ![]() ���룩
���룩
�����⣬��OM��OB��һ��ֱ���ϣ�![]() ����ON��OB��һ��ֱ���ϣ�
����ON��OB��һ��ֱ���ϣ�![]() ����OM��OA��һ��ֱ���ϣ�
����OM��OA��һ��ֱ���ϣ�![]() �������ٽ�λ��
�������ٽ�λ��
�ٵ�![]() ʱ����ͼ1��ʾ
ʱ����ͼ1��ʾ
��ʱ��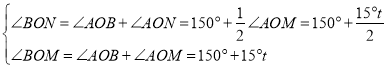
��![]() Ϊ��ֵ
Ϊ��ֵ
�ڵ�![]() ʱ����ͼ2��ʾ
ʱ����ͼ2��ʾ
��ʱ��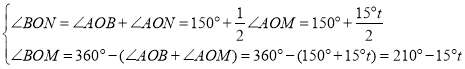
��![]() ��Ϊ��ֵ
��Ϊ��ֵ
�۵�![]() ʱ����ͼ3��ʾ
ʱ����ͼ3��ʾ
��ʱ��
��![]() Ϊ��ֵ
Ϊ��ֵ
�ܵ�![]() ʱ����ͼ4��ʾ
ʱ����ͼ4��ʾ
��ʱ��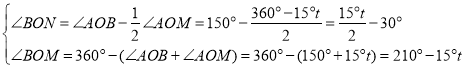
��![]() ��Ϊ��ֵ
��Ϊ��ֵ
���ϣ���![]() ��
��![]() ʱ��
ʱ��![]() Ϊ��ֵ��
Ϊ��ֵ��


 ��ʿһ��ȫͨϵ�д�
��ʿһ��ȫͨϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��x=��4��x�ύ�ڵ�E��һ�������ϵ������߹�ԭ�㽻�߶�OE�ڵ�A����ֱ��x=��4�ڵ�B����B��ƽ����x���ֱ���������߽��ڵ�C��ֱ��OC��ֱ��AB��D����AD��BD=1��3��
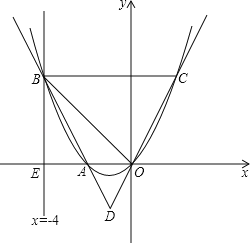
��1�����A�����ꣻ
��2������OBC�ǵ��������Σ���������ߵĺ�����ϵʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����AOB �� ��������A��O��B����ʹ��A��O��B��=��AOB �� ������
����________ΪԲ�ģ�________Ϊ�뾶�������ֱ�OA �� OB�ڵ�C �� D ��
�ڻ�һ������O��A������________ΪԲ�ģ�________��Ϊ�뾶��������O��A���ڵ�C�䣬
���Ե�________ΪԲ��________��Ϊ�뾶���������2���������Ļ����ڵ�D�䣮
�ܹ���________������O��B�������A��O��B��=��AOB ��
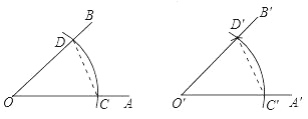
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ��֯��һ��ѧ������Բ���������Ƿ������Լ����̺ͷ�������Ⱥ�������ڹ����������̵�̬�ȣ������ࣺA��ʾ������ֹ��B��ʾ���е�����ֹ��C��ʾ����ν���������ʾ����飬���ݵ������ֱ��������������ͳ��ͼ. �����ͼ���ṩ����Ϣ����������⣺
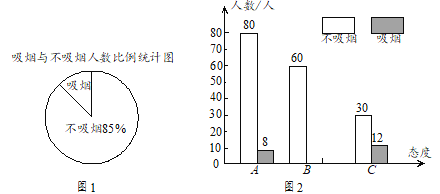
��1��ͼ1�У������̡���������ռ���ε�Բ�ĽǵĶ����Ƕ��٣�
��2����α�����������ж����ˣ�
��3����ȫ����ͳ��ͼ��
��4�������й�������480���ˣ�����д�Լ�ж��������̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���뾶Ϊ1��СԲ��뾶Ϊ2�Ĵ�Բ����һ����������ԭ���غϣ���Բ���������������Ĺ�����СԲ���˶��ٶ�Ϊÿ��������λ����Բ���˶��ٶ�Ϊÿ��2������λ��
��1������Բ�������������1�ܣ����Բ�������غϵĵ�����ʾ������������
��2����СԲ��������Բ���������ع������涨��Բ���ҹ���ʱ���Ϊ�������������ʱ���Ϊ���������ι����������¼���£���λ���룩����1��+2����4����2��+3����8
�ٵڼ��ι�����Բ��ԭ����Զ��
�ڵ���Բ�����˶�ʱ����Բ�˶���·�̹��ж��٣���ʱ��Բ�������غϵĵ�֮��ľ����Ƕ��٣��������������
��3������Բͬʱ�������ϸ�������ijһ������������������һ��ʱ�����Բ�������غϵĵ�֮�����9�������ʱ��Բ�������غϵĵ�����ʾ������

![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij������ÿ�칩Ӧ������������㹽��˰�����ɳ����������ɫ����.ijһ�죬�ð����̹���������6000�����Ҹ�����ӵ����������ͼ��ʾ��������˵����ȷ����( )

A.���칲�������������2000��B.�����㹽��˰��������ǹ�ɳ����3��
C.����������ɫ������ͳ��ͼ������Ӧ��Բ�Ľ���![]() D.�ݴ˿��Եó���������ӭ�İ����Ǻ��������
D.�ݴ˿��Եó���������ӭ�İ����Ǻ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���۲�����ͼ�εı仯���̣�����������⣺


��ͼ������ABC�У�DΪBC���ϵ�һ���㣨D�㲻��B��C�����غϣ���DE��AC��AB��E�㣬DF��AB��AC��F�㣮
��С��1����̽��AD����ʲô����ʱ���ı���AEDFΪ���Σ���˵�����ɣ�
��С��2���ڣ�1���������£���ABC����ʲô����ʱ���ı���AEDFΪ�����Σ�Ϊʲô��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��ABC��ֱ��PQ��ֱƽ��AC�����AB����E������CE������C��CFƽ����BA��PQ�ڵ�F������AF��
��1����֤����AED�ա�CFD��
��2����֤���ı���AECF�����Σ�
��3����AD=3��AE=5��������AECF������Ƕ��٣�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ֽƬABCD�У�AD��5��AB��3����MΪ����AD�ϵ�һ�����㣬����ABM��BM�۵��õ���NBM������NBC��ֱ�������Σ������з���������M������Ӧ��AM���ȵĺ�Ϊ______��
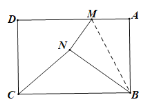
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com