
【题目】观察下列图形的变化过程,解答以下问题:


如图,在△ABC中,D为BC边上的一动点(D点不与B、C两点重合).DE∥AC交AB于E点,DF∥AB交AC于F点.
(小题1)试探索AD满足什么条件时,四边形AEDF为菱形,并说明理由;
(小题2)在(1)的条件下,△ABC满足什么条件时,四边形AEDF为正方形?为什么?
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在直角梯形ABCD中,AB∥CD,AD⊥AB,∠B=60°,AB=10,BC=4,点P沿线段AB从点A向点B运动,设AP=x.

(1)求AD的长;
(2)点P在运动过程中,是否存在以A、P、D为顶点的三角形与以P、C、B为顶点的三角形相似?若存在,求出x的值;若不存在,请说明理由;
(3)设△ADP与△PCB的外接圆的面积分别为S1、S2,若S=S1+S2,求S的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A=﹣xy+x+1,B=4x+3y,
(1)当x=﹣2, y=0.6时,求A+2B的值;
(2)若代数式2A﹣B的结果与字母y的取值无关,求x的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() ,
,![]() 为
为![]() 内部的一条射线,
内部的一条射线,![]() .
.
(1)如图1,若![]() 平分
平分![]() ,
,![]() 为
为![]() 内部的一条射线,
内部的一条射线,![]() ,求
,求![]() 的度数;
的度数;

(2)如图2,若射线![]() 绕着
绕着![]() 点从
点从![]() 开始以每秒
开始以每秒![]() 的速度顺时针旋转至
的速度顺时针旋转至![]() 结束、
结束、![]() 绕着
绕着![]() 点从
点从![]() 开始以每秒
开始以每秒![]() 的速度逆时针旋转至
的速度逆时针旋转至![]() 结束,当一条射线到达终点时另一条射线也停止运动.若运动时间为
结束,当一条射线到达终点时另一条射线也停止运动.若运动时间为![]() 秒,当
秒,当![]() 时,求
时,求![]() 的值;
的值;

(3)若射线![]() 绕着
绕着![]() 点从
点从![]() 开始以每秒
开始以每秒![]() 的速度逆时针旋转至
的速度逆时针旋转至![]() 结束,在旋转过程中,
结束,在旋转过程中,![]() 平分
平分![]() ,试问
,试问![]() 在某时间段内是否为定值;若不是,请说明理由;若是,请补全图形,并直接写出这个定值以及
在某时间段内是否为定值;若不是,请说明理由;若是,请补全图形,并直接写出这个定值以及![]() 相应所在的时间段.(本题中的角均为大于
相应所在的时间段.(本题中的角均为大于![]() 且小于
且小于![]() 的角)
的角)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠1=∠2,要说明△ABD≌△ACD,还需从下列条件中选一个,错误的选法是( )
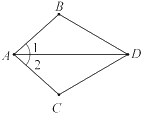
A. ∠ADB=∠ADCB. ∠B=∠CC. DB=DCD. AB=AC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(8,0)及在第四象限的动点P(x,y),且x+y=10,设△OPA的面积为S
(1) 求S关于x的函数表达式,并直接写出x的取值范围
(2) 画出函数S的图象
(3) S=12时,点P坐标为
查看答案和解析>>
科目:初中数学 来源: 题型:
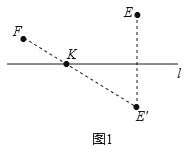
【题目】如图1,点EF在直线l的同一侧,要在直线l上找一点K,使KE与KF的距离之和最小,我们可以作出点E关于l的对称点E′,连接FE′交直线L于点K,则点K即为所求.
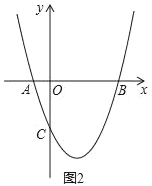
(1)(实践运用)抛物线y=ax2+bx+c经过点A(﹣1,0)、B(3,0)、C(0,﹣3).如图2.
①求该抛物线的解析式;
②在抛物线的对称轴上找一点P,使PA+PC的值最小,并求出此时点P的坐标及PA+PC的最小值.
(2)(知识拓展)在对称轴上找一点Q,使|QA﹣QC|的值最大,并求出此时点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国庆期间,王老师计划组织朋友去晋西北游览两日.经了解,现有甲、乙两家旅行社针对组团两日游的游客报价均为每人500元,且提供的服务完全相同.甲旅行社表示,每人都按八五折收费;乙旅行社表示,若人数不超过20人,每人都按九折收费,超过20人,则超出部分每人按八折收费.假设组团参加甲、乙两家旅行社两日游的人数均为![]() 人.
人.
(1)请列式表示甲、乙两家旅行社收取组团两日游的总费用;
(2)若王老师组团参加两日游的人数共有30人,请你通过计算,在甲、乙两家旅行社中,帮助王老师选择收取总费用较少的一家.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com