
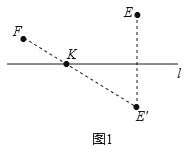
【题目】如图1,点EF在直线l的同一侧,要在直线l上找一点K,使KE与KF的距离之和最小,我们可以作出点E关于l的对称点E′,连接FE′交直线L于点K,则点K即为所求.
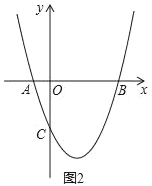
(1)(实践运用)抛物线y=ax2+bx+c经过点A(﹣1,0)、B(3,0)、C(0,﹣3).如图2.
①求该抛物线的解析式;
②在抛物线的对称轴上找一点P,使PA+PC的值最小,并求出此时点P的坐标及PA+PC的最小值.
(2)(知识拓展)在对称轴上找一点Q,使|QA﹣QC|的值最大,并求出此时点Q的坐标.
【答案】(1)①y=x2﹣2x﹣3,②点P的坐标为(1,﹣2),PA+PC的最小值为3![]() ;(2)点Q的坐标为(1,﹣6).
;(2)点Q的坐标为(1,﹣6).
【解析】分析:(1)①由点A、B的坐标可将抛物线的解析式变形为交点式,代入点C的坐标即可求出a值,此题得解;
②由点A、B关于抛物线的对称轴对称可得出连接BC交抛物线对称轴于点P,此时PA+PC的值最小,根据抛物线的解析式可求出其对称轴为直线x=1,由点B、C的坐标利用待定系数法可求出过点B、C的直线的解析式,代入x=1求出y值,由此即可得出点P的坐标,再利用勾股定理求出线段BC的长即可;
(2)连接AC并延长AC交抛物线对称轴与点Q,此时|QA﹣QC|的值最大,且|QA﹣QC|的最大值为线段AC的长(三角形两边之差小于第三边),由点A、C的坐标利用待定系数法可求出过点A、C的直线的解析式,代入x=1求出y值,由此即可得出点Q的坐标,此题得解.
详解:(1)①∵抛物线与x轴的交点为A(﹣1,0)、B(3,0),∴抛物线的解析式为y=a(x+1)(x﹣3).
∵抛物线过点C(0,﹣3),∴﹣3=(0+1)×(0﹣3)a,∴a=1,∴该抛物线的解析式为y=(x+1)(x﹣3)=x2﹣2x﹣3.
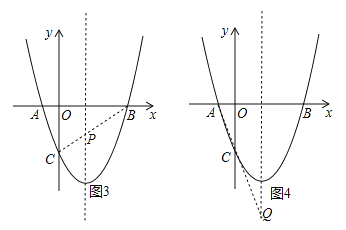
②∵点A、B关于抛物线的对称轴对称,∴连接BC交抛物线对称轴于点P,此时PA+PC的值最小,如图3所示.
∵抛物线的解析式为y=x2﹣2x﹣3=(x﹣1)2﹣4,∴抛物线的对称轴为直线x=1.
利用待定系数法可求出过点B、C的直线为y=x﹣3,当x=1时,y=x﹣3=1﹣3=﹣2,∴点P的坐标为(1,﹣2),PA+PC的最小值为BC=![]() =3
=3![]() .
.
(2)连接AC并延长AC交抛物线对称轴与点Q,此时|QA﹣QC|的值最大,且|QA﹣QC|的最大值为线段AC的长,如图4所示.
利用待定系数法可求出过点A、C的直线为y=﹣3x﹣3,当x=1时,y=﹣3x﹣3=﹣3×1﹣3=﹣6,∴点Q的坐标为(1,﹣6).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
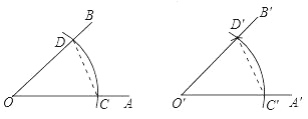
【题目】已知,∠AOB . 求作:∠A′O′B′,使∠A′O′B′=∠AOB . 作法:
①以________为圆心,________为半径画弧.分别交OA , OB于点C , D .
②画一条射线O′A′,以________为圆心,________长为半径画弧,交O′A′于点C′,
③以点________为圆心________长为半径画弧,与第2步中所画的弧交于点D′.
④过点________画射线O′B′,则∠A′O′B′=∠AOB .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列图形的变化过程,解答以下问题:


如图,在△ABC中,D为BC边上的一动点(D点不与B、C两点重合).DE∥AC交AB于E点,DF∥AB交AC于F点.
(小题1)试探索AD满足什么条件时,四边形AEDF为菱形,并说明理由;
(小题2)在(1)的条件下,△ABC满足什么条件时,四边形AEDF为正方形?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC,直线PQ垂直平分AC,与边AB交于E,连接CE,过点C作CF平行于BA交PQ于点F,连接AF.
(1)求证:△AED≌△CFD;
(2)求证:四边形AECF是菱形.
(3)若AD=3,AE=5,则菱形AECF的面积是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,以下几种说法中:①![]() 和
和![]() 是同位角;②
是同位角;②![]() 和
和![]() 是同位角;③
是同位角;③![]() 和
和![]() 是内错角;④
是内错角;④![]() 和
和![]() 是同旁内角;⑤
是同旁内角;⑤![]() 和
和![]() 是同位角;⑥
是同位角;⑥![]() 和
和![]() 是同位角;正确的个数是( )
是同位角;正确的个数是( )

A.3B.4C.5D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司计划购买A、B两种计算器共100个,要求A种计算器数量不低于B种的![]() ,且不高于B种的
,且不高于B种的![]() .已知买1个A种计算器和1个B种计算器共需250元,买2个A种计算器和3个B种计算器的费用相等。
.已知买1个A种计算器和1个B种计算器共需250元,买2个A种计算器和3个B种计算器的费用相等。
(1)求两种计算器的单价。
(2)求如何购买可使总费用最低。
(3)由于市场行情波动,实际购买时,A种计算器单价下调m元(m>0),同时B种计算器单价上调了m元,此时购买这两种计算器所需最少费用为12200元,求m的值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD向右平移一段距离后得到四边形![]() .
.

(1)找出图中存在的平行且相等的四条线段(即四条线段全部互相平行且相等);
(2)找出图中存在的四组相等的角;
(3)四边形ABCD与四边形![]() 的形状、大小相同吗?为什么?
的形状、大小相同吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
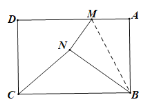
【题目】如图,矩形纸片ABCD中,AD=5,AB=3.若M为射线AD上的一个动点,将△ABM沿BM折叠得到△NBM.若△NBC是直角三角形.则所有符合条件的M点所对应的AM长度的和为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论: ① c=0;②该抛物线的对称轴是直线x=﹣1;③当x=1时,y=2a;④am![]() +bm+a>0(m≠﹣1);⑤设A(100,y),B(﹣100,y
+bm+a>0(m≠﹣1);⑤设A(100,y),B(﹣100,y![]() )在该抛物线上,则y>y
)在该抛物线上,则y>y![]() .其中正确的结论有___________ .(写出所有正确结论的序号)
.其中正确的结论有___________ .(写出所有正确结论的序号)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com