
【题目】如图,直线x=﹣4与x轴交于点E,一开口向上的抛物线过原点交线段OE于点A,交直线x=﹣4于点B,过B且平行于x轴的直线与抛物线交于点C,直线OC交直线AB于D,且AD:BD=1:3.
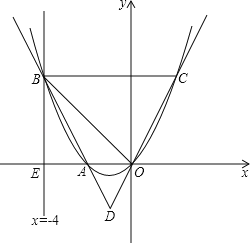
(1)求点A的坐标;
(2)若△OBC是等腰三角形,求此抛物线的函数关系式.
【答案】(1)(﹣2,0);(2)y=![]() x2+
x2+![]() x或y=
x或y=![]() x2+
x2+![]() x.
x.
【解析】
试题分析:(1)过点D作DF⊥x轴于点F,由抛物线的对称性可知OF=AF,则2AF+AE=4①,由DF∥BE,得到△ADF∽△ABE,根据相似三角形对应边成比例得出![]() =
=![]() ,即AE=2AF②,①与②联立组成二元一次方程组,解出AE=2,AF=1,进而得到点A的坐标;
,即AE=2AF②,①与②联立组成二元一次方程组,解出AE=2,AF=1,进而得到点A的坐标;
(2)先由抛物线过原点(0,0),设此抛物线的解析式为y=ax2+bx,再根据抛物线过原点(0,0)和A点(﹣2,0),求出对称轴为直线x=﹣1,则由B点横坐标为﹣4得出C点横坐标为2,BC=6.再由OB>OC,可知当△OBC是等腰三角形时,可分两种情况讨论:①当OB=BC时,设B(﹣4,y1),列出方程,解方程求出y1的值,将A,B两点坐标代入y=ax2+bx,运用待定系数法求出此抛物线的解析式;②当OC=BC时,设C(2,y2),列出方程,解方程求出y2的值,将A,C两点坐标代入y=ax2+bx,运用待定系数法求出此抛物线的解析式.
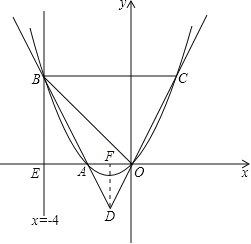
试题解析:(1)如图,过点D作DF⊥x轴于点F.
由题意,可知OF=AF,则2AF+AE=4①.
∵DF∥BE,
∴△ADF∽△ABE,
∴![]() =
=![]() ,即AE=2AF②,
,即AE=2AF②,
①与②联立,解得AE=2,AF=1,
∴点A的坐标为(﹣2,0);
(2)∵抛物线过原点(0,0),
∴可设此抛物线的解析式为y=ax2+bx.
∵抛物线过原点(0,0)和A点(﹣2,0),
∴对称轴为直线x=![]() =﹣1,
=﹣1,
∵B、C两点关于直线x=﹣1对称,B点横坐标为﹣4,
∴C点横坐标为2,
∴BC=2﹣(﹣4)=6.
∵抛物线开口向上,
∴∠OAB>90°,OB>AB=OC,
∴当△OBC是等腰三角形时,分两种情况讨论:
①当OB=BC时,设B(﹣4,y1),
则16+![]() =36,解得y1=±2
=36,解得y1=±2![]() (负值舍去).
(负值舍去).
将A(﹣2,0),B(﹣4,2![]() )代入y=ax2+bx,
)代入y=ax2+bx,
得![]() ,解得
,解得![]() .
.
∴此抛物线的解析式为y=![]() x2+
x2+![]() x;
x;
②当OC=BC时,设C(2,y2),
则4+![]() =36,解得y2=±4
=36,解得y2=±4![]() (负值舍去).
(负值舍去).
将A(﹣2,0),C(2,4![]() )代入y=ax2+bx,
)代入y=ax2+bx,
得![]() ,解得
,解得![]() .
.
∴此抛物线的解析式为y=![]() x2+
x2+![]() x.
x.
综上可知,若△OBC是等腰三角形,此抛物线的函数关系式为y=![]() x2+
x2+![]() x或y=
x或y=![]() x2+
x2+![]() x.
x.


科目:初中数学 来源: 题型:
【题目】已知a是不为1的有理数,我们把![]() 称为a的差倒数,如2的差倒数是
称为a的差倒数,如2的差倒数是![]() =-1.现已知a1=
=-1.现已知a1=![]() ,a2是a1的差倒数,a3是a2的差倒数,a4是a3的差倒数.
,a2是a1的差倒数,a3是a2的差倒数,a4是a3的差倒数.
(1)求a2,a3,a4的值.
(2)根据(1)的计算结果,请猜想并写出a2018·a2019·a2020的值.
(3)计算:a1+a2+a3+…+a2018+a2019.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=![]() ﹣x﹣4与坐标轴相交于A、B、C三点,P是线段AB上一动点(端点除外),过P作PD∥AC,交BC于点D,连接CP.
﹣x﹣4与坐标轴相交于A、B、C三点,P是线段AB上一动点(端点除外),过P作PD∥AC,交BC于点D,连接CP.

(1)直接写出A、B、C的坐标;
(2)求抛物线y=![]() ﹣x﹣4的对称轴和顶点坐标;
﹣x﹣4的对称轴和顶点坐标;
(3)求△PCD面积的最大值,并判断当△PCD的面积取最大值时,以PA、PD为邻边的平行四边形是否为菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:![]() 是关于
是关于 ![]() ,
,![]() 的多项式,如果
的多项式,如果 ![]() ,那么
,那么 ![]() 叫做“对称多项式”.例如,如果
叫做“对称多项式”.例如,如果 ![]() ,则
,则 ![]() 显然 ,所以
显然 ,所以 ![]() 是“对称多项式”.
是“对称多项式”.
(1)![]() 是“对称多项式”,试说明理由;
是“对称多项式”,试说明理由;
(2)请写一个“对称多项式”,![]() (不多于四项);
(不多于四项);
(3)如果 ![]() 和
和 ![]() 均为“对称多项式”,那么
均为“对称多项式”,那么 ![]() 一定是“对称多项式”吗?如果一定,请说明理由,如果不一定,请举例说明.
一定是“对称多项式”吗?如果一定,请说明理由,如果不一定,请举例说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小学时候大家喜欢玩的幻方游戏,老师稍加创新改成了“幻圆”游戏,现在将﹣1、2、﹣3、4、﹣5、6、﹣7、8分别填入图中的圆圈内,使横、竖以及内外两圈上的4个数字之和都相等,老师已经帮助同学们完成了部分填空,则图中a+b的值为( )

A. ﹣6或﹣3 B. ﹣8或1 C. ﹣1或﹣4 D. 1或﹣1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B、C、D四个车站的位置如图所示,A、B两站之间的距离AB=a﹣b,B、C两站之间的距离BC=2a﹣b,B、D两站之间的距离BD=![]() .
.
(1)求A、C两站之间的距离AC.
(2)若A、C两站之间的距离AC=90km,求C、D两站之间的距离CD.
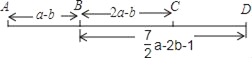
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角梯形ABCD中,AB∥CD,AD⊥AB,∠B=60°,AB=10,BC=4,点P沿线段AB从点A向点B运动,设AP=x.

(1)求AD的长;
(2)点P在运动过程中,是否存在以A、P、D为顶点的三角形与以P、C、B为顶点的三角形相似?若存在,求出x的值;若不存在,请说明理由;
(3)设△ADP与△PCB的外接圆的面积分别为S1、S2,若S=S1+S2,求S的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由于数学课上需要用到科学计算器,班级决定集体购买,班长小明先去文具店购买了2个A型计算器和3个B型计算器,共花费90元;后又买了1个A型计算器和2个B型计算器,共花费55元(每次两种计算器的售价都不变)
(1)求A型计算器和B型计算器的售价分别是每个多少元?
(2)经统计,班内还需购买两种计算器共40个,设购买A型计算器t个,所需总费用w元,请求出w关于t的函数关系式;
(3)要求:B型计算器的数量不少于A型计数器的2倍,请设计一种购买方案,使所需总费用最低.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() ,
,![]() 为
为![]() 内部的一条射线,
内部的一条射线,![]() .
.
(1)如图1,若![]() 平分
平分![]() ,
,![]() 为
为![]() 内部的一条射线,
内部的一条射线,![]() ,求
,求![]() 的度数;
的度数;

(2)如图2,若射线![]() 绕着
绕着![]() 点从
点从![]() 开始以每秒
开始以每秒![]() 的速度顺时针旋转至
的速度顺时针旋转至![]() 结束、
结束、![]() 绕着
绕着![]() 点从
点从![]() 开始以每秒
开始以每秒![]() 的速度逆时针旋转至
的速度逆时针旋转至![]() 结束,当一条射线到达终点时另一条射线也停止运动.若运动时间为
结束,当一条射线到达终点时另一条射线也停止运动.若运动时间为![]() 秒,当
秒,当![]() 时,求
时,求![]() 的值;
的值;

(3)若射线![]() 绕着
绕着![]() 点从
点从![]() 开始以每秒
开始以每秒![]() 的速度逆时针旋转至
的速度逆时针旋转至![]() 结束,在旋转过程中,
结束,在旋转过程中,![]() 平分
平分![]() ,试问
,试问![]() 在某时间段内是否为定值;若不是,请说明理由;若是,请补全图形,并直接写出这个定值以及
在某时间段内是否为定值;若不是,请说明理由;若是,请补全图形,并直接写出这个定值以及![]() 相应所在的时间段.(本题中的角均为大于
相应所在的时间段.(本题中的角均为大于![]() 且小于
且小于![]() 的角)
的角)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com