
【题目】如图,在等腰Rt△ABC中,∠CAB=90°,P是△ABC内一点,且PA=1,PB=3,PC= ![]() .求:∠CPA的大小
.求:∠CPA的大小

【答案】∠CPA=135°
【解析】
由于△ABC为等腰直角三角形,AB=AC,则把△APB绕A点逆时针旋转90°可得到△AP′C,连PP′,根据旋转的性质得到∠P′AP=90°,P′A=PA=1,P′C=PB=3,得到△PAP′为等腰直角三角形,根据等腰直角三角形的性质得P′P=![]() PA=
PA=![]() ,∠APP′=45°,在△P′PC中,可得到PC2+P′P2=P′C2,根据勾股定理的逆定理得到△P′PC为直角三角形,∠CPP′=90°,利用∠CPA=∠CPP′+∠APP′进行计算即可.
,∠APP′=45°,在△P′PC中,可得到PC2+P′P2=P′C2,根据勾股定理的逆定理得到△P′PC为直角三角形,∠CPP′=90°,利用∠CPA=∠CPP′+∠APP′进行计算即可.
∵△ABC为等腰直角三角形,AB=AC,
∴把△APB绕A点逆时针旋转90°可得到△AP′C,连PP′,如图,
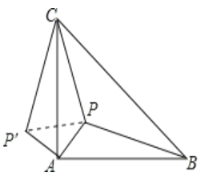
∴∠P′AP=90°,P′A=PA=1,P′C=PB=3,
∴△PAP′为等腰直角三角形,
∴P′P=![]() PA=
PA=![]() ,∠APP′=45°,
,∠APP′=45°,
在△P′PC中,P′C=3,P′P=![]() ,PC=
,PC=![]() ,
,
∵![]() ,
,
∴PC2+P′P2=P′C2,
∴△P′PC为直角三角形,∠CPP′=90°,
∴∠CPA=∠CPP′+∠APP′=90°+45°=135°.


 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:
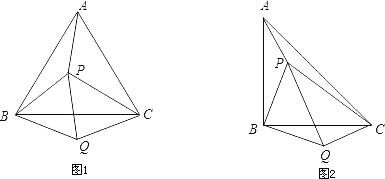
【题目】(1)如图①所示,P是等边△ABC内的一点,连接PA、PB、PC,将△BAP绕B点顺时针旋转60°得△BCQ,连接PQ.若PA2+PB2=PC2,证明∠PQC=90°;
(2)如图②所示,P是等腰直角△ABC(∠ABC=90°)内的一点,连接PA、PB、PC,将△BAP绕B点顺时针旋转90°得△BCQ,连接PQ.当PA、PB、PC满足什么条件时,∠PQC=90°?请说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形OABC的两边OA、OC分别在x轴、y轴上,点D(5,3)在边AB上,以C为中心,把△CDB旋转90°,则旋转后点D的对应点D′的坐标是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四位同学做“读语句画图”练习.甲同学读语句“直线经过A,B,C三点,且点C在点A与点B之间”,画出图形(1);乙同学读语句“两条线段AB,CD相交于点P”画出图形(2);丙同学读语句“点P在直线l上,点Q在直线l外”画出图形(3);丁同学读语句“点M在线段AB的延长线上,点N在线段AB的反向延长线上”画出图形(4).其中画的不正确的是( )

A. 甲同学B. 乙同学C. 丙同学D. 丁同学
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两城相距800千米,一辆客车从甲城开往乙城,车速为![]() 千米
千米![]() 小时,同时一辆出租车从乙城开往甲城,车速为90千米
小时,同时一辆出租车从乙城开往甲城,车速为90千米![]() 小时,设客车行驶时间为
小时,设客车行驶时间为![]() 小时
小时![]()
![]() 当
当![]() 时,客车与乙城的距离为多少千米
时,客车与乙城的距离为多少千米![]() 用含a的代数式表示
用含a的代数式表示![]()
![]() 已知
已知![]() ,丙城在甲、乙两城之间,且与甲城相距260千米
,丙城在甲、乙两城之间,且与甲城相距260千米
![]() 求客车与出租车相距100千米时客车的行驶时间;
求客车与出租车相距100千米时客车的行驶时间;![]() 列方程解答
列方程解答![]()
![]() 已知客车和出租车在甲、乙之间的服务站M处相遇时,出租车乘客小王突然接到开会通知,需要立即返回,此时小王有两种返回乙城的方案:
已知客车和出租车在甲、乙之间的服务站M处相遇时,出租车乘客小王突然接到开会通知,需要立即返回,此时小王有两种返回乙城的方案:
方案一:继续乘坐出租车到丙城,加油后立刻返回乙城,出租车加油时间忽略不计;
方案二:在M处换乘客车返回乙城.
试通过计算,分析小王选择哪种方案能更快到达乙城?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校准备建一条5米宽的文化长廊,并按下图方式铺设边长为1米的正方形地砖,图中阴影部分为彩色地砖,白色部分为普通地砖.

(1)如果长廊长8米,则需要彩色地砖 块,普通地砖 块;
(2)如果长廊长2a米(a为正整数),则需要彩色地砖 块;
(3)购买时,恰逢地砖市场地砖促销,彩色地砖原价为100元/块,普通地砖原价为40元/块,优惠方案为:买一块彩色地砖赠送一块普通地砖.
①如果长廊长x米(x为整数),用含x代数式表示购买地砖所需的钱数;
②当x=51米时,求购买地砖所需钱数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有8筐杨梅,以每筐5千克为标准,超过的千克数记作正数,不足的千克数记作负数,称后的记录如下:

回答下列问题:
(1)这8筐杨梅中,最接近5千克的那筐杨梅为多少千克?
(2)以每筐5千克为标准,这8筐杨梅总计超过多少千克或者不足多少千克?
(3)若杨梅每千克售价25元,则出售这8筐杨梅可卖多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线l![]() 经过A(2,3)B(
经过A(2,3)B(![]() ,0)
,0)
(1) 求直线l![]() 的解析式及l
的解析式及l![]() 与坐标轴围成的图形的面积.
与坐标轴围成的图形的面积.
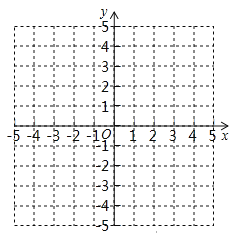
(2) 将l![]() 向下平移3个单位长度,再向左平移1个单位长度,得到直线l
向下平移3个单位长度,再向左平移1个单位长度,得到直线l![]() ,画出l
,画出l![]() 的图象并直接写出l
的图象并直接写出l![]() 的解析式__________________.
的解析式__________________.
(3)若点M(![]() ,m),N(n,1)在直线l
,m),N(n,1)在直线l![]() 上,P为y轴上一动点,则PM+PN最小时,P的坐标为____________,此时PM+PN=______________.
上,P为y轴上一动点,则PM+PN最小时,P的坐标为____________,此时PM+PN=______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人在一条直线道路上分别从相距1500米的A,B 两点同时出发,相向而行,当两人相遇后,甲继续向点B前进(甲到达点B时停止运动),乙也立即向B点返回.在整个运动过程中,甲、乙均保持匀速运动.甲、乙两人之间的距离y(米)与乙运动的时间x(秒) 之间的关系如图所示.则甲到B点时,乙距B点的距离是________米.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com