
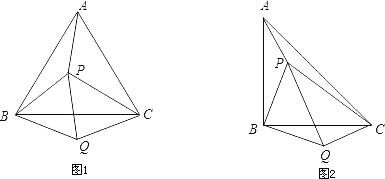
【题目】(1)如图①所示,P是等边△ABC内的一点,连接PA、PB、PC,将△BAP绕B点顺时针旋转60°得△BCQ,连接PQ.若PA2+PB2=PC2,证明∠PQC=90°;
(2)如图②所示,P是等腰直角△ABC(∠ABC=90°)内的一点,连接PA、PB、PC,将△BAP绕B点顺时针旋转90°得△BCQ,连接PQ.当PA、PB、PC满足什么条件时,∠PQC=90°?请说明.
【答案】(1)证明见解析(2)满足:![]()
【解析】
由旋转得△BAP≌△BCQ 满足:![]()
∴PA=CQ PB=BQ 由旋转得△BAP≌△BCQ
∵∠PBQ=60![]() ∴PA=CQ PB=BQ
∴PA=CQ PB=BQ
∴△PBQ为等边三角形 ∠PBQ=![]()
∴PB=PQ ∴![]()
∵PA![]() +PB
+PB![]() =PC
=PC![]() ∵
∵![]()
∴![]() ∴
∴![]()
∴∠PQC=90![]() ∴
∴![]()
(1)由旋转的性质可得到的条件是:①BP=BQ、PA=QC,②∠ABP=∠CBQ;
由②可证得∠PBQ=∠CBP+∠CBQ=∠CBP+∠ABP=∠ABC=60°,联立BP=BQ,即可得到△BPQ是等边三角形的结论,则BP=PQ;将等量线段代换后,即可得出PQ2+QC2=PC2,由此可证得∠PQC=90°;
(2)由(1)的解题思路知:△PBQ是等腰Rt△,则PQ2=2PB2,其余过程同(1),只不过所得结论稍有不同.


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案科目:初中数学 来源: 题型:
【题目】某校对七、八、九年级的学生进行体育水平测试,成绩评定为优秀、良好、合格、不合格四个等第.为了解这次测试情况,学校从三个年级随机抽取200名学生的体育成绩进行统计分析.相关数据的统计图、表如下:
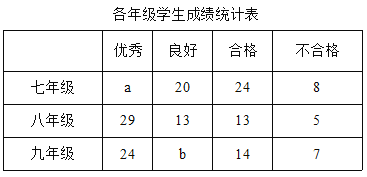

根据以上信息解决下列问题:
(1)在统计表中,a的值为 ,b的值为 ;
(2)在扇形统计图中,八年级所对应的扇形圆心角为 度;
(3)若该校三个年级共有2000名学生参加考试,试估计该校学生体育成绩不合格的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在等腰梯形ABCD中,AD//BC,E是AB的中点,过点E作EF//BC交CD于点F,AB=4,BC=6,∠B=60°.
(1)求点E到BC的距离;
(2)点P为线段EF上的一个动点,过点P作PM⊥EF交BC于M,过M作MN//AB交折线ADC于N,连结PN,设EP=x.
①当点N在线段AD上时(如图2),△PMN的形状是否发生改变?若不变,求出△PMN的周长;若改变,请说明理由;
②当点N在线段DC上时(如图3),是否存在点P,使△PMN为等腰三角形?若存在,请求出所有满足条件的x的值;若不存在,请说明理由.



图1 图2 图3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上的A、B两点分别对应数字a、b,且a、b满足|4a-b|+(a-4)2=0
![]()
(1)a= ,b= ,并在数轴上面出A、B两点;
(2)若点P从点A出发,以每秒3个单位长度向x轴正半轴运动,求运动时间为多少时,点P到点A的距离是点P到点B距离的2倍;
(3)数轴上还有一点C的坐标为30,若点P和点Q同时从点A和点B出发,分别以每秒3个单位长度和每秒1个单位长度的速度向C点运动,P点到达C点后,再立刻以同样的速度返回,运动到终点A.求点P和点Q运动多少秒时,P、Q两点之间的距离为4,并求此时点Q对应的数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若a,b,c是直角三角形的三条边长,斜边c上的高的长是h,给出下列结论:
①以a2,b2,c2的长为边的三条线段能组成一个三角形
②以![]() ,
, ![]() ,
, ![]() 的长为边的三条线段能组成一个三角形
的长为边的三条线段能组成一个三角形
③以a+b,c+h,h的长为边的三条线段能组成直角三角形
④以![]() ,
, ![]() ,
, ![]() 的长为边的三条线段能组成直角三角形
的长为边的三条线段能组成直角三角形
其中所有正确结论的序号为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
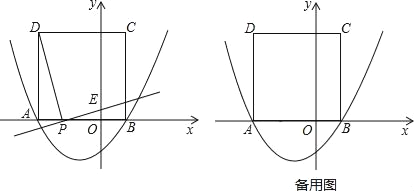
【题目】如图,已知二次函数y=![]() x2+bx﹣
x2+bx﹣![]() 与x轴交于点A(﹣3,0)和点B,以AB为边在x轴上方作正方形ABCD,点P是x轴上一动点,连接DP,过点P作DP的垂线与y轴交于点E.
与x轴交于点A(﹣3,0)和点B,以AB为边在x轴上方作正方形ABCD,点P是x轴上一动点,连接DP,过点P作DP的垂线与y轴交于点E.
(1)试求出二次函数的表达式和点B的坐标;
(2)当点P在线段AO(点P不与A、O重合)运动至何处时,线段OE的长有最大值,求出这个最大值;
(3)是否存在这样的点P,使△PED是等腰三角形?若存在,请求出点P的坐标及此时△PED与正方形ABCD重叠部分的面积;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系中,O为坐标原点,已知A(-1,1),在坐标轴上确定点P,使△AOP为等腰三角形,则符合条件的点P的个数共有( )
A. 10个 B. 8个 C. 4个 D. 6个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com