
【题目】如图,已知二次函数y=![]() x2+bx﹣
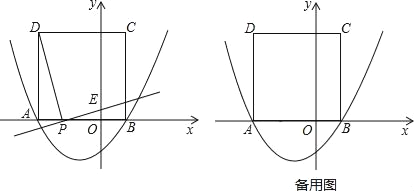
x2+bx﹣![]() 与x轴交于点A(﹣3,0)和点B,以AB为边在x轴上方作正方形ABCD,点P是x轴上一动点,连接DP,过点P作DP的垂线与y轴交于点E.
与x轴交于点A(﹣3,0)和点B,以AB为边在x轴上方作正方形ABCD,点P是x轴上一动点,连接DP,过点P作DP的垂线与y轴交于点E.
(1)试求出二次函数的表达式和点B的坐标;
(2)当点P在线段AO(点P不与A、O重合)运动至何处时,线段OE的长有最大值,求出这个最大值;
(3)是否存在这样的点P,使△PED是等腰三角形?若存在,请求出点P的坐标及此时△PED与正方形ABCD重叠部分的面积;若不存在,请说明理由.
【答案】(1)![]() ,B(1,0);(2)
,B(1,0);(2)![]() ;(3)点P的坐标为(4,0)时,此 时△PED与正方形ABCD重叠部分的面积为
;(3)点P的坐标为(4,0)时,此 时△PED与正方形ABCD重叠部分的面积为![]() .
.
【解析】分析:(1)将点A的坐标代入二次函数的解析式求得其解析式,然后求得点B的坐标即可求得正方形ABCD的边长,从而求得点D的纵坐标.
(2)PA=t,OE=l,利用△DAP∽△POE得到比例式,从而得到有关两个变量的二次函数,求最值即可.
(3)分点P位于y轴左侧和右侧两种情况讨论即可得到重叠部分的面积.
详解:(1)将点A(﹣3,0)代入y=![]() x2+bx﹣
x2+bx﹣![]() 得
得![]() ﹣3b﹣
﹣3b﹣![]() =0,解得b=1,
=0,解得b=1,
∴二次函数的表达式为y=![]() x2+x﹣
x2+x﹣![]() ,
,
当y=0时,![]() x2+x﹣
x2+x﹣![]() =0,解得x1=1,x2=﹣3,
=0,解得x1=1,x2=﹣3,
∴B(1,0);
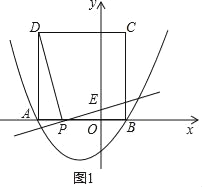
(2)设PA=t(﹣3<t<0),则OP=3﹣t,如图1,
∵DP⊥PE,
∴∠DPA=∠PEO,
∴△DAP∽△POE,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
∴OE=﹣![]() t2+
t2+![]() t
t
=﹣![]() (t﹣
(t﹣![]() )2+
)2+![]() ,
,
∴当t=![]() 时,OE有最大值,即P为AO中点时,OE的最大值为
时,OE有最大值,即P为AO中点时,OE的最大值为![]() ;
;
(3)存在.
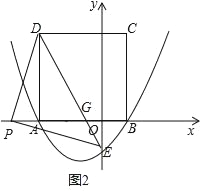
当点P在y轴左侧时,如图2,DE交AB于G点,
∵PD=PE,∠DPE=90°,
∴△DAP≌△POE,
∴PO=AD=4,
∴PA=1,OE=1,
∵AD∥OE,
∴![]() =
=![]() =4,
=4,
∴AG=![]() ,
,
∴S△DAG=![]()
![]() 4=
4=![]() ,
,
∴P点坐标为(﹣4,0),此时△PED与正方形ABCD重叠部分的面积为![]() ;
;
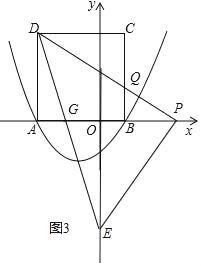
当P点在y轴右侧时,如图3,DE交AB于G点,DP与BC相交于Q,
同理可得△DAP≌△POE,
∴PO=AD=4,
∴PA=7,OE=7,
∵AD∥OE,
∴![]() =
=![]() =
=![]() ,
,
∴OG=![]() ,
,
同理可得BQ=![]()
∴S四边形DGBQ=![]() ×(
×(![]() +1)×4+
+1)×4+![]() ×4×
×4×![]() =
=![]()
∴当点P的坐标为(4,0)时,此时△PED与正方形ABCD重叠部分的面积为![]() .
.


科目:初中数学 来源: 题型:
【题目】某跳水队为了解运动员的年龄情况,作了一次年龄调查,根据跳水运动员的年龄(单位:岁),绘制出如下的统计图①和图②.请根据相关信息,解答下列问题:

(1)本次接受调查的跳水运动员人数为 ,图①中![]() 的值为 ;
的值为 ;
(2)求统计的这组跳水运动员年龄数据的平均数、众数和中位数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图①所示,P是等边△ABC内的一点,连接PA、PB、PC,将△BAP绕B点顺时针旋转60°得△BCQ,连接PQ.若PA2+PB2=PC2,证明∠PQC=90°;
(2)如图②所示,P是等腰直角△ABC(∠ABC=90°)内的一点,连接PA、PB、PC,将△BAP绕B点顺时针旋转90°得△BCQ,连接PQ.当PA、PB、PC满足什么条件时,∠PQC=90°?请说明.
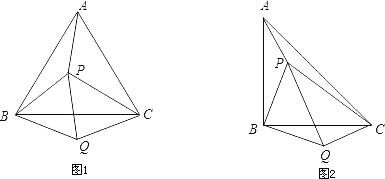
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列结沦中,错误的有( )
①Rt△ABC中,已知两边分别为3和4,则第三边的长为5;②三角形的三边分别为a、b、c,若a2+b2=c2,则∠A=90°;③若△ABC中,∠A:∠B:∠C=1:5:6,则这个三角形是一个直角三角形;④若(x﹣y)2+M=(x+y)2成立,则M=4xy.
A. 0个 B. 1个 C. 2个 D. 3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,菱形ABCD中,∠A=60°,点P从A出发,以2cm/s的速度沿边AB、BC、CD匀速运动到D终止,点Q从A与P同时出发,沿边AD匀速运动到D终止,设点P运动的时间为t(s).△APQ的面积S(cm2)与t(s)之间函数关系的图象由图2中的曲线段OE与线段EF、FG给出.
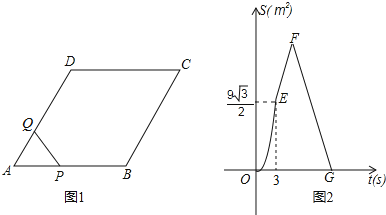
(1)求点Q运动的速度;
(2)求图2中线段FG的函数关系式;
(3)问:是否存在这样的t,使PQ将菱形ABCD的面积恰好分成1:5的两部分?若存在,求出这样的t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,矩形ABCD的边AD在y轴上,抛物线![]() 经过点A、点B,与x轴交于点E、点F,且其顶点M在CD上。
经过点A、点B,与x轴交于点E、点F,且其顶点M在CD上。
(1)请直接写出下列各点的坐标:
A ,B ,C ,D ;
(2)若点P是抛物线上一动点(点P不与点A、点B重合),过点P作![]() 轴的平行线l与直线AB交于点G,与直线BD交于点H,如图2。
轴的平行线l与直线AB交于点G,与直线BD交于点H,如图2。
①当线段PH=2GH时,求点P的坐标;
②当点P在直线BD下方时,点K在直线BD上,且满足△KPH∽△AEF,求△KPH面积的最大值。
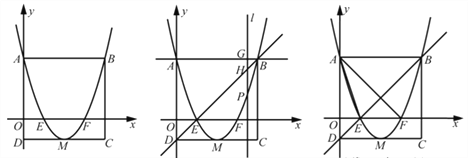
图1 图2 备用图
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形OABC的两边OA、OC分别在x轴、y轴上,点D(5,3)在边AB上,以C为中心,把△CDB旋转90°,则旋转后点D的对应点D′的坐标是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有8筐杨梅,以每筐5千克为标准,超过的千克数记作正数,不足的千克数记作负数,称后的记录如下:

回答下列问题:
(1)这8筐杨梅中,最接近5千克的那筐杨梅为多少千克?
(2)以每筐5千克为标准,这8筐杨梅总计超过多少千克或者不足多少千克?
(3)若杨梅每千克售价25元,则出售这8筐杨梅可卖多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com