
【题目】如图,已知一次函数y=k1x+b的图象分别与x轴、y轴的正半轴交于 A,B 两点,且与反比例函数y=![]() 交于 C,E 两点,点 C 在第二象限,过点 C 作CD⊥x轴于点 D,AC=2
交于 C,E 两点,点 C 在第二象限,过点 C 作CD⊥x轴于点 D,AC=2![]() ,OA=OB=1.
,OA=OB=1.

(1)△ADC 的面积;
(2)求反比例函数y= ![]() 与一次函数的y=k1x+b表达式.
与一次函数的y=k1x+b表达式.
【答案】(1)2;(2)反比例函数的表达式为y=﹣![]() ;一次函数的表达式为y=﹣x+1.
;一次函数的表达式为y=﹣x+1.
【解析】试题分析:(1)求出![]() 解直角三角形求出
解直角三角形求出![]() 根据三角形的面积公式求出即可;
根据三角形的面积公式求出即可;
(2)把C的坐标代入反比例函数的解析式,即可求出![]() ,把
,把![]() 的坐标代入一次函数的解析式,即可求出b和k1.
的坐标代入一次函数的解析式,即可求出b和k1.
试题解析:(1)∵OA=OB,
![]() ,
,
∵CD⊥x轴于D,
∴![]() ,
,
∴![]() ,
,
∴CD=AD,
∵![]()
∴![]()
∴△ADC的面积为: ![]()
(2)∵OA=1,AD=2,
∴OD=1,
∵CD=2,
∴C的坐标为(1,2),
∵点C在反比例函数![]() 的图象上,
的图象上,
∴![]()
∴![]()
∴反比例函数的表达式为![]()
∵一次函数![]() 过B(0,1),C(1,2),
过B(0,1),C(1,2),
∴代入得: ![]()
解得: ![]()
∴一次函数的表达式为y=x+1.


科目:初中数学 来源: 题型:
【题目】某校准备建一条5米宽的文化长廊,并按下图方式铺设边长为1米的正方形地砖,图中阴影部分为彩色地砖,白色部分为普通地砖.

(1)如果长廊长8米,则需要彩色地砖 块,普通地砖 块;
(2)如果长廊长2a米(a为正整数),则需要彩色地砖 块;
(3)购买时,恰逢地砖市场地砖促销,彩色地砖原价为100元/块,普通地砖原价为40元/块,优惠方案为:买一块彩色地砖赠送一块普通地砖.
①如果长廊长x米(x为整数),用含x代数式表示购买地砖所需的钱数;
②当x=51米时,求购买地砖所需钱数.
查看答案和解析>>
科目:初中数学 来源: 题型:
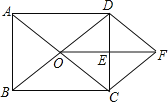
【题目】已知:如图,在矩形ABCD中,对角线AC、BD相交于点O,E是CD中点,连结OE.过点C作CF∥BD交线段OE的延长线于点F,连结DF.求证:
(1)△ODE≌△FCE;
(2)四边形ODFC是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形![]() 中,点
中,点![]() 、
、![]() 是正方形内两点,
是正方形内两点,![]() ,
,![]() ,为探索这个图形的特殊性质,某数学兴趣小组经历了如下过程:
,为探索这个图形的特殊性质,某数学兴趣小组经历了如下过程:

(1)在图1中,连接![]() ,且
,且![]()
①求证:![]() 与
与![]() 互相平分;
互相平分;
②求证:![]() ;
;
(2)在图2中,当![]() ,其它条件不变时,
,其它条件不变时,![]() 是否成立?若成立,请证明:若不成立,请说明理由.
是否成立?若成立,请证明:若不成立,请说明理由.

(3)在图3中,当![]() ,
,![]() ,
,![]() 时,求
时,求![]() 之长.
之长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人在一条直线道路上分别从相距1500米的A,B 两点同时出发,相向而行,当两人相遇后,甲继续向点B前进(甲到达点B时停止运动),乙也立即向B点返回.在整个运动过程中,甲、乙均保持匀速运动.甲、乙两人之间的距离y(米)与乙运动的时间x(秒) 之间的关系如图所示.则甲到B点时,乙距B点的距离是________米.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】骰子是一种特别的数字立方体(见下图),它符合规则:相对两面的点数之和总是7,下面四幅图中可以折成符合规则的骰子的是( )
![]()
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】发现问题、探索规律,要有一双敏锐的双眼,下面的图形是由边长为1的小正方形按照某种规律排列而成的.

(1)观察图形,填写下表:
图形个数(n) | (1) | (2) | (3) |
正方形的个数 | 8 |
|
|
图形的周长 | 18 |
|
|
(2)推测第n个图形中,正方形有 个,周长为 .
(3)写出第30个图形的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一快递员需要在规定时间内开车将快递送到某地,若快递员开车每分钟行驶1.2![]() ,就早到10分钟;若快递员开车每分钟行驶0.8
,就早到10分钟;若快递员开车每分钟行驶0.8![]() ,就要迟到5分钟.试求出规定时间及快递员所行驶的总路程.
,就要迟到5分钟.试求出规定时间及快递员所行驶的总路程.
小明和小新在解答时先设出未知数,然后列出方程如下:
![]() ①,
①,![]() ②,其中方程①由小明所列,方程②由小新所列.
②,其中方程①由小明所列,方程②由小新所列.
(1)小明所设![]() 表示 ;
表示 ;
小新所设![]() 表示 .
表示 .
(2)请选小明或小新的方法写出完整的解答过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中:
①0是最小的整数;
②有理数不是正数就是负数;
③正整数、负整数、正分数、负分数统称为有理数;
④非负数就是正数;
⑤![]() 不仅是有理数,而且是分数;
不仅是有理数,而且是分数;
⑥![]() 是无限不循环小数,所以不是有理数;
是无限不循环小数,所以不是有理数;
⑦无限小数不都是有理数;
⑧正数中没有最小的数,负数中没有最大的数.
其中错误的说法的个数为( )
A.7个B.6个C.5个D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com