
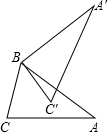
 如图,在△ABC中,AB=AC,将△ABC绕点B逆时针方向旋转60°,得到△A′BC′,若A′C′⊥AB,则∠ABC′的度数为15°.
如图,在△ABC中,AB=AC,将△ABC绕点B逆时针方向旋转60°,得到△A′BC′,若A′C′⊥AB,则∠ABC′的度数为15°. 分析 先根据旋转的性质得∠ABA′=∠CBC′=60°,∠A=∠A′,再由A′C′⊥AB,则根据互余可计算出∠A′=30°,则∠A=30°,接着根据等腰三角形的性质和三角形内角和定理计算出∠ABC=∠C=75°,然后计算∠ABC-∠CBC′即可.
解答 解:∵△ABC绕点B逆时针方向旋转60°得到△A′BC′,
∴∠ABA′=∠CBC′=60°,∠A=∠A′,
∵A′C′⊥AB,
∴∠A′=90°-60°=30°,
∴∠A=30°,
∵AB=AC,
∴∠ABC=∠C=$\frac{1}{2}$(180°-30°)=75°,
∴∠ABC′=∠ABC-∠CBC′=75°-60°=15°.
故答案为15°.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了等腰三角形的性质.


 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案科目:初中数学 来源: 题型:解答题
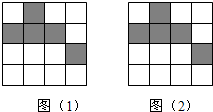 如图(1)、(2)分别是由16个小正方形组成的正方形网格图,现已将其中部分小正方形涂黑,请你用两种不同的方法,分别在两个图中再涂黑两个空白的小正方形,使它(涂黑部分)成为轴对称图形.
如图(1)、(2)分别是由16个小正方形组成的正方形网格图,现已将其中部分小正方形涂黑,请你用两种不同的方法,分别在两个图中再涂黑两个空白的小正方形,使它(涂黑部分)成为轴对称图形.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4,2 | B. | 1,3 | C. | 2,3 | D. | 5,2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
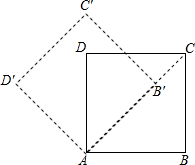 如图,将边长为$2+\sqrt{2}$的正方形ABCD绕点A逆时针方向旋转45°至AB′C′D′,若CD和B′C′相交于点E,则CE=2.
如图,将边长为$2+\sqrt{2}$的正方形ABCD绕点A逆时针方向旋转45°至AB′C′D′,若CD和B′C′相交于点E,则CE=2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com