
分析 首先利用勾股定理得出直角边的长,再利用直角三角形面积求法得出答案.
解答 解:在直角三角形中,根据勾股定理:
另一条直角边长为:$\sqrt{{{(2\sqrt{6}+\sqrt{3})}^2}-{{(\sqrt{6}+2\sqrt{3})}^2}}$=3(cm).
故直角三角形的面积为:
S=$\frac{1}{2}$×3×($\sqrt{6}+2\sqrt{3}$)=$\frac{3}{2}$$\sqrt{6}+3\sqrt{3}$(cm2)
答:这个直角三角形的面积为($\frac{3}{2}$$\sqrt{6}+3\sqrt{3}$)cm2.
点评 此题主要考查了二次根式的应用,正确应用勾股定理是解题关键.


科目:初中数学 来源: 题型:解答题
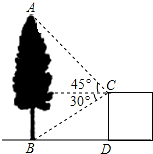 如图,在建筑平台CD的顶部C处,测得大树AB的顶部A的仰角为45°,测得大树AB的底部B的俯角为30°,已知平台CD的高度为6m,求大树的高度为多少m?(结果保留根号)
如图,在建筑平台CD的顶部C处,测得大树AB的顶部A的仰角为45°,测得大树AB的底部B的俯角为30°,已知平台CD的高度为6m,求大树的高度为多少m?(结果保留根号)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 去括号 | B. | 移项 | C. | 合并同类项 | D. | 系数化为1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
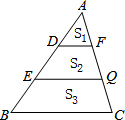 如图,在△ABC中,DF∥EQ∥BC,且AD=DE=EB,△ABC被DF、EQ分成三部分,且三部分面积分别为S1,S2,S3,则S1:S2:S3=1:3:5.
如图,在△ABC中,DF∥EQ∥BC,且AD=DE=EB,△ABC被DF、EQ分成三部分,且三部分面积分别为S1,S2,S3,则S1:S2:S3=1:3:5.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com