
分析 根据题意可知抛物线的顶点坐标,故可设抛物线解析式为y=a(x-2)2+6,将点(-4,0)代入求得a的值即可.
解答 解:根据题意设抛物线解析式为y=a(x-2)2+6,
将点(-4,0)代入,得:36a+6=0,
解得:a=-$\frac{1}{6}$,
∴y=-$\frac{1}{6}$(x-2)2+6=-$\frac{1}{6}$x2+$\frac{2}{3}$x+$\frac{16}{3}$,
故答案为:y=-$\frac{1}{6}$x2+$\frac{2}{3}$x+$\frac{16}{3}$.
点评 本题主要考查待定系数法求二次函数解析式,在利用待定系数法求二次函数关系式时,要根据题目给定的条件,选择恰当的方法设出关系式,从而代入数值求解.一般地,当已知抛物线上三点时,常选择一般式,用待定系数法列三元一次方程组来求解;当已知抛物线的顶点或对称轴时,常设其解析式为顶点式来求解;当已知抛物线与x轴有两个交点时,可选择设其解析式为交点式来求解.


科目:初中数学 来源: 题型:选择题
 甲、乙两人从科技馆出发,沿相同的路线分别以不同的速度匀速跑向极地馆,甲先跑一段路程后,乙开始出发,当乙超出甲150米时,乙停在此地等候甲,两人相遇后乙又继续以原来的速度跑向极地馆.如图是甲、乙两人在跑步的全过程中经过的路程y(米)与甲出发的时间x(秒)的函数图象.则下列四种说法:①甲的速度为1.5米/秒;②a=750;③乙在途中等候甲100秒;④乙出发后第一次与甲相遇时乙跑了375米.其中正确的个数是( )
甲、乙两人从科技馆出发,沿相同的路线分别以不同的速度匀速跑向极地馆,甲先跑一段路程后,乙开始出发,当乙超出甲150米时,乙停在此地等候甲,两人相遇后乙又继续以原来的速度跑向极地馆.如图是甲、乙两人在跑步的全过程中经过的路程y(米)与甲出发的时间x(秒)的函数图象.则下列四种说法:①甲的速度为1.5米/秒;②a=750;③乙在途中等候甲100秒;④乙出发后第一次与甲相遇时乙跑了375米.其中正确的个数是( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
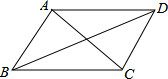 如图,在下列四组条件中,不能判断AD∥BC的是( )
如图,在下列四组条件中,不能判断AD∥BC的是( )| A. | ∠DAC=ACB | B. | ∠ADB=∠DBC | C. | ∠DAB+∠ABC=180° | D. | ∠BAC=∠ACD |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,两个反比例函数y1=$\frac{k}{x}$(k>0)和y=$\frac{1}{x}$在第一象限内的图象依次是C1和C2,设点P在C1上,PC⊥x轴于点C,交C2于点A,PD⊥y轴于点D,交C2于点B,若四边形PAOB的面积为3,则k=4.
如图,两个反比例函数y1=$\frac{k}{x}$(k>0)和y=$\frac{1}{x}$在第一象限内的图象依次是C1和C2,设点P在C1上,PC⊥x轴于点C,交C2于点A,PD⊥y轴于点D,交C2于点B,若四边形PAOB的面积为3,则k=4.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com