【题目】如图，给正五边形的顶点依次编号为1，2，3，4，5．若从某一顶点开始，沿正五边形的边顺时针方向行走，顶点编号的数字是几，就走几个边长，则称这种走法为一次“移位”．如：小宇在编号为3的顶点上时，那么他应走3个边长，即从3→4→5→1为第一次“移位”，这时他到达编号为1的顶点；然后从1→2为第二次“移位”．若小宇从编号为2的顶点开始，第15次“移位”后，则他所处顶点的编号为__．
科目：初中数学 来源： 题型：
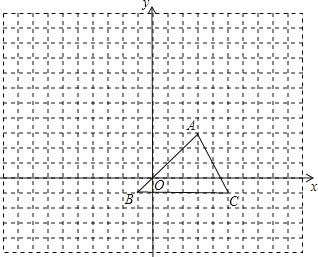
【题目】如图所示的正方形网格，△ABC的顶点在网格上，在建立平面直角坐标系后，点B的坐标是(-1，-1)
(1)把△ABC向左平移10格得到
，画出；
(2)画出关于x轴对称的图形
；
(3)把△ABC绕点C顺时针旋转90°后得到
，画出，并写出点
的坐标.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】有这样一个问题：探究函数
的图象与性质.下面是小文的探究过程，请补充完整：
（1）函数的自变量
的取值范围是__________；
（2）下表是
与的几组对应值：
如图，在平面直角坐标系
中，描出了以上表中各对应值为坐标的点.
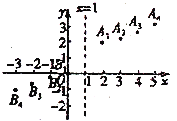
①观察图中各点的位置发现：点
和
，
和
，
和
，
和
均关于某点中心对称，则该点的坐标为__________；
②小文分析函数表达式发现：当
时，该函数的最大值为0，则该函数图象在直线
左侧的最高点的坐标为__________；
（3）小文补充了该函数图象上两个点
，
.
①在上图中描出这两个点，并画出该函数的图象；
②写出该函数的一条性质：__________.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在
中，已知
，
为
的角平分线.\
（1）如图1，当
时，在
边上截取
，连接
，你能发现线段、
、
之间有怎样的数量关系么？请直接写出你的发现：________________________（不需要证明）；
（2）如图2，当
时，线段、、还有（1）中的数量关系么？请证明你的猜想；
（3）如图3，当为的外角平分线时，线段、、又有怎样的数量关系？不需要证明，请直接写出你的猜想：______________________.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，矩形ABCO中，点C在x轴上，点A在y轴上，点B的坐标是（一6，8）．矩形ABCO沿直线BD折叠，使得点A落在对角线OB上的点E处，折痕与OA、x轴分别交于点D、F．
(1)直接写出线段BO的长：
(2)求点D的坐标；
(3)若点N是平面内任一点，在x轴上是否存在点M，使咀M、N、E、O为顶点的四边形是菱形？若存在，请直接写出满足条件的点M的坐标：若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
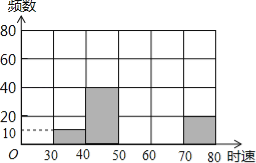
【题目】将某雷达测速区监测到的一组汽车的时速数据整理，得到其频数分布表（未完成）：
数据段 | 30～40 | 40～50 | 50～60 | 60～70 | 70～80 | 总计 |
频 数 | 10 | 40 | | | 20 | |
百分比 | 5% | | 40% | | 10% | |
注：30～40为时速大于等于30千米而小于40千米，其他类同．
（1）请你把表中的数据填写完整；
（2）补全频数分布直方图；
（3）如果此路段汽车时速超过60千米即为违章，则违章车辆共有多少辆？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某校八年级640名学生在“计算机应用”培训前、后各参加了一次水平相同的测试，并以同一标准分成“不合格”、“合格”、“优秀”3个等级，为了解培训效果，用抽样调查的方式从中抽取32名学生的2次测试等级，并绘制成条形统计图：
（1）这32名学生经过培训，测试等级“不合格”的百分比比培训前减少了多少？
（2）估计该校八年级学生中，培训前、后等级为“合格”与“优秀”的学生各有多少名？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
