
【题目】已知,关于![]() ,
,![]() 的方程组
的方程组![]() 的解满足
的解满足![]() ,
,![]() .
.
(1)求![]() 的取值范围;
的取值范围;
(2)化简![]() ;
;
(3)若![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)a的取值范围是![]() <a<2;
<a<2;
(2)|a2||a+1|=2a+1;
(3)m的取值范围是5<m<5.
【解析】
(1)把a看做已知数表示出方程组的解,根据x≥0,y<0,求出a的范围即可;
(2)根据(1)中的取值可解答;
(3)先根据幂的性质将已知变形得:x+2y=m,再将方程组化为x+2y的形式可得结论.
(1)解方程组![]() ,得:
,得:![]() ,
,
∵x≥0,y<0,
∴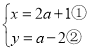 ,
,
解不等式①,得:a>![]() ,
,
解不等式②,得:a<2,
∴a的取值范围是![]() <a<2;
<a<2;
(2)∵![]() <a<2,
<a<2,
∴|a2||a+1|=2a(a+1)=2a+1;
(3)3x9y=3m,
3x(32)y=3m,
3x+2y=3m,
x+2y=m,
∵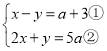 ,
,
②①得:x+2y=4a3,
即m=4a3,
∵a的取值范围是![]() <a<2,
<a<2,
2<4a<8,
5<4a3<5,
∴m的取值范围是5<m<5.


科目:初中数学 来源: 题型:
【题目】操作题
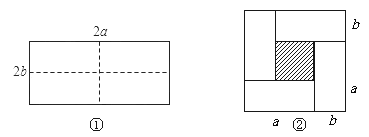
(1)如图①所示是一个长为2a,宽为2b的矩形,若把此图沿图中虚线用剪刀均分为四块小长方形,然后按图②的形状拼成一个正方形,请问:这两个图形的 不变.图②中阴影部分的面积用含a、b的代数式表示为_________________;
(2)由(1)的探索中,可得到的结论是:在周长一定的矩形中,___________时,面积最大;
(3)若一矩形的周长为36 cm,则当边长为多少时,该图形的面积最大?最大面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)把数轴补充完整.
(2)在数轴上表示下列各数.
(3)用“<”连接起来. .
(4)﹣|﹣2|与﹣4之间的距离是 .
3![]() ,﹣4,﹣(﹣1.5),﹣|﹣2|
,﹣4,﹣(﹣1.5),﹣|﹣2|
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,BC的垂直平分线EF交∠ABC的平分线BD于E,如果∠BAC=60°,∠ACE=24°,那么∠BCE的大小是( )

A. 24° B. 30° C. 32° D. 36°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,点A,B,C,D在一条直线上,填写下列空格:
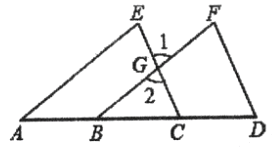
∵AE∥BF(已知)
∴∠E=∠1(______________________)
∵∠E=∠F(已知〉
∴∠_____=∠F(________________)
∴________∥_________(________________________)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践
问题情境
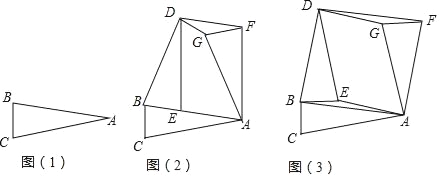
在综合实践课上,老师让同学们“以三角形的旋转”为主题进行数学活动,如图(1),在三角形纸片ABC中,AB=AC,∠B=∠C=α.
操作发现
(1)创新小组将图(1)中的△ABC以点B为旋转中心,逆时针旋转角度α,得到△DBE,再将△ABC以点A为旋转中心,顺时针旋转角度α,得到△AFG,连接DF,得到图(2),则四边形AFDE的形状是 .
(2)实践小组将图(1)中的△ABC以点B为旋转中心,逆时针逆转90°,得到△DBE,再将△ABC以点A为旋转中心,顺时针旋转90°,得到△AFG,连接DF、DG、AE,得到图(3),发现四边形AFDB为正方形,请你证明这个结论.
拓展探索
(3)请你在实践小组操作的基础上,再写出图(3)中的一个特殊四边形,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
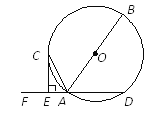
【题目】如图,AB是⊙O的直径,AD是⊙O的弦,点F是DA延长线上的一点,过⊙O上一点C作⊙O的切线交DF于点E,CE⊥DF.
(1)求证:AC平分∠FAB;
(2)若AE=1,CE=2,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有190张铁皮做盒子,每张铁皮可做8个盒身或22个盒底,一个盒身与两个盒底配成一个完整的盒子,(一张铁皮只能生产一种产品)
(1)向用多少张铁皮做盒身,多少张铁皮做盒底,可以正好用完190张铁皮并制成一批完整的盒子?
(2)这批盒子一共有多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一张矩形纸板按图中虚线裁剪成九块,其中有两块是边长都为![]() 的大正方形,两块是边长都为
的大正方形,两块是边长都为![]() 的小正方形,五块是长为
的小正方形,五块是长为![]() 、宽为
、宽为![]() 的全等小矩形,且
的全等小矩形,且![]() >
> ![]() .(以上长度单位:cm)
.(以上长度单位:cm)
(1)观察图形,可以发现代数式![]() 可以因式分解为 ;
可以因式分解为 ;
(2)若每块小矩形的面积为10![]() ,四个正方形的面积和为58
,四个正方形的面积和为58![]() ,试求图中所有裁剪线(虚线部分)长之和.
,试求图中所有裁剪线(虚线部分)长之和.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com