
【题目】如图1,在△ABC中,∠BAC=90°,AB=AC,M、N是过点A的一条直线,作 BD⊥MN于点D,CE⊥MN于点E。

(1)求证:DE=BD+CE;
(2)当直线MN绕点A旋转到图2所示的位置,其他条件不变,则BD与DE、CE的关系如何?请予以证明

【答案】(1)证明见解析(2)BD=DE+CE
【解析】试题分析:(1)由题中条件可得Rt△ABD≌Rt△CAE,再由线段之间的关系写出最终结论即可;
(2)由HL得出Rt△ABD≌Rt△CAE,进而得出BD=AE,AD=CE,再由线段之间的转化即可得出结论:BD=DE+CE或DE=BD-CE.
试题解析:
(1)∵BD⊥直线MN,CE⊥直线MN,
∴∠BDA=∠AEC=90°,
∵∠BAC=90°,
∴∠BAD+∠CAE=90°,
∵∠BAD+∠ABD=90°,
∴∠CAE=∠ABD,
∵在△ADB和△CEA中
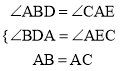
∴△ADB≌△CEA
∴AE=BD,AD=CE,
∴DE=AE+AD=BD+CE;
(2)关系:BD=DE+CE
证明如下:
∵BD⊥直线MN,CE⊥直线MN,
∴∠BDA=∠AEC=90°,
∵∠BAC=90°,
∴∠BAD+∠CAE=90°,
∵∠BAD+∠ABD=90°,
∴∠CAE=∠ABD,
∵在△ADB和△CEA中
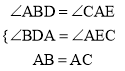
∴△ADB≌△CEA
∴AE=BD,AD=CE,
∴BD=AE=DE+AD=DE+CE.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:初中数学 来源: 题型:
【题目】为了参加中考体育测试,甲,乙,丙三位同学进行足球传球训练,球从一个人脚下随机传到另一个人脚下,且每位传球人传球给其余两人的机会是均等的,由甲开始传球,共传三次.
(l)求请用树状图列举出三次传球的所有可能情况:
(2)传球三次后,球回到甲脚下的概率;
(3)三次传球后,球回到甲脚下的概率大还是传到乙脚下的概率大?
查看答案和解析>>
科目:初中数学 来源: 题型:
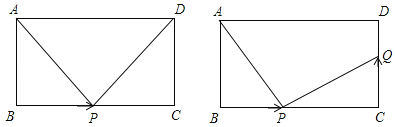
【题目】如图,在长方形ABCD中,AB=CD=6cm,BC=10cm,点P从点B出发,以2cm/秒的速度沿BC向点C运动,设点P的运动时间为t秒:
(1)PC=______cm.(用t的代数式表示)
(2)当t为何值时,△ABP≌△DCP?
(3)当点P从点B开始运动,同时,点Q从点C出发,以v cm/秒的速度沿CD向点D运动,是否存在这样v的值,使得△ABP与△PQC全等?若存在,请求出v的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系中,已知点 A(a+b,2-a)与点B(a-5,b-2a)关于y轴对称.
(1)求A、B两点的坐标;
(2)如果点B关于x轴的对称点是C,在图中标出点A、B、C,并求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】到三角形三顶点距离相等的点是( ),到三角形三边距离相等的点是( )
A. 三条角平分线的交点,三条垂直平分线的交点
B. 三条角平分线的交点,三条中线的交点
C. 三条垂直平分线的交点,三条中线的交点
D. 三条垂直平分线的交点,三条角平分线的交点
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分8分)2014年12月28日“青烟威荣”城际铁路正式开通,从烟台到北京的高铁里程比普快里程缩短了81千米,运行时间减少了9小时,已知烟台到北京的普快列车里程月1026千米,高铁平均时速是普快平均时速的2.5倍.
(1)求高铁列车的平均时速;
(2)某日王老师要去距离烟台大约630千米的某市参加14:00召开的会议,如果他买到
当日8:40从烟台到该是的高铁票,而且从该市火车站到会议地点最多需要1.5小时.试问在高铁列车准点到达的情况下他能在开会之前赶到吗?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com