
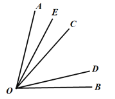
【题目】如图,已知∠AOB=75°,∠COD=35°,∠COD在∠AOB的内部绕着点O旋转(OC与OA不重合,OD与OB不重合),若OE为∠AOC的角平分线.则2∠BOE-∠BOD的值为______.
科目:初中数学 来源: 题型:
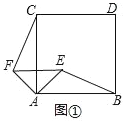
【题目】(1)如图①,四边形ABDC是正方形,以A为顶点,作等腰直角三角形△AEF,∠EAF=90°,线段BE与CF之间的数量关系为:_____.(直接写出结果,不需要证明)
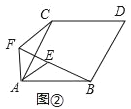
(2)如图②,四边形ABDC是菱形,以A为顶点,作等腰三角形△AEF,AE=AF,∠BAC=∠EAF,(1)中结论成立吗?若成立,请证明;若不成立,请说明理由.
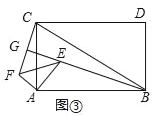
(3)如图③,四边形ABDC是矩形,以A为顶点,作直角三角形△AEF,∠EAF=90°,AB=![]() AC,AE=
AC,AE=![]() AF,当∠EAB=60°时,延长BE交CF于点G.
AF,当∠EAB=60°时,延长BE交CF于点G.
①求证:BE⊥CF;
②当AB=12,AE=4时,求线段BG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
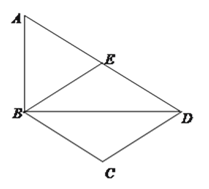
【题目】如图,在Rt△ABD中,∠ABD=90°,AB=1,sin∠ADB=![]() ,点E为AD的中点,线段BA绕点B顺时针旋转到BC(旋转角小于180°),使BC∥AD.连接DC,BE.
,点E为AD的中点,线段BA绕点B顺时针旋转到BC(旋转角小于180°),使BC∥AD.连接DC,BE.
(1)则四边形BCDE是________,并证明你的结论;
(2)求线段AB旋转过程中扫过的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】未成年人思想道德建设越来越受到社会的关注.某青少年研究机构随机调查了某校 100名学生寒假花零花钱的数量(钱数取整数元),以便引导学生树立正确的消费观.根据调查 数据制成了如下的频数分布表(部分空格未填).
某校 100 名学生寒假花零花钱数量的频数分布表:
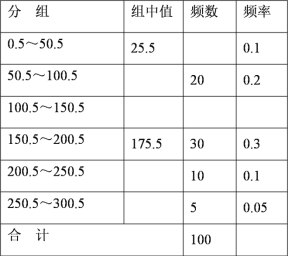
(1)完成该频数分布表;
(2)画出频数分布直方图.
(3)研究认为应对消费 150 元以上的学 生提出勤俭节约的建议.试估计应对该校1200 学生中约多少名学生提出该项建议?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从泰州乘“K”字头列车A、“T”字头列车B都可直达南京,已知A车的平均速度为80 km/h,B车的平均速度为A车的1.5倍,且行完全程B车所需时间比A车少40分钟.
(1)求泰州至南京的铁路里程;
(2)若两车以各自的平均速度分别从泰州、南京同时相向而行,问经过多少时间两车相距40 km?
查看答案和解析>>
科目:初中数学 来源: 题型:
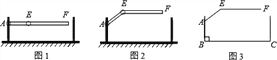
【题目】某地下车库出口处安装了“两段式栏杆”,如图1所示,点A是栏杆转动的支点,点E是栏杆两段的联结点![]() 当车辆经过时,栏杆AEF最多只能升起到如图2所示的位置,其示意图如图3所示
当车辆经过时,栏杆AEF最多只能升起到如图2所示的位置,其示意图如图3所示![]() 栏杆宽度忽略不计
栏杆宽度忽略不计![]() ,其中
,其中![]() 米,那么适合该地下车库的车辆限高标志牌为
米,那么适合该地下车库的车辆限高标志牌为
(参考数据:![]()
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
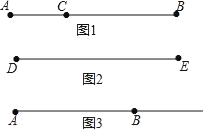
【题目】定义:若线段上的一个点把这条线段分成1:2的两条线段,则称这个点是这条线段的三等分点.如图1,点C在线段AB上,且AC:CB=1:2,则点C是线段AB的一个三等分点,显然,一条线段的三等分点有两个.
(1)已知:如图2,DE=15cm,点P是DE的三等分点,求DP的长.
(2)已知,线段AB=15cm,如图3,点P从点A出发以每秒1cm的速度在射线AB上向点B方向运动;点Q从点B出发,先向点A方向运动,当与点P重合后立马改变方向与点P同向而行且速度始终为每秒2cm,设运动时间为t秒.
①若点P点Q同时出发,且当点P与点Q重合时,求t的值.
②若点P点Q同时出发,且当点P是线段AQ的三等分点时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校计划购买篮球、排球共20个,购买2个篮球,3个排球,共需花费190元;购买3个篮球的费用与购买5个排球的费用相同。
(1)篮球和排球的单价各是多少元?
(2)若购买篮球不少于8个,所需费用总额不超过800元.请你求出满足要求的所有购买方案,并直接写出其中最省钱的购买方案
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com