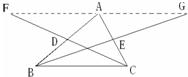
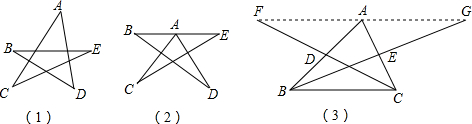
解:(1)
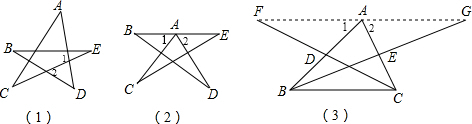
180°;
(2)∠CAD+∠B+∠C+∠D+∠E的和不变,仍然为180°.理由如下:
∵∠1=∠C+∠E,∠2=∠B+∠D,
而∠1+∠CAD+∠2=180°,
∴∠CAD+∠B+∠C+∠D+∠E=180°;
(3)F、A、G三点在一条直线上.理由如下:
∵点D为AB的中点,
∴AD=BD,
又∵∠ADF=∠BDC,DF=CD,
∴△ADF≌△BDC,
∴∠1=∠DBC,
同理可得△AGE≌△CBE,
∴∠2=∠ECB,
∵∠ABC+∠ACB+∠BAC=180°,
∴∠1+∠2+∠BAC=180°,
∴F、A、G三点在一条直线上.
分析:(1)根据三角形内角和定理得到∠A+∠C+∠1=180°,再根据三角形外角性质得到∠1=∠2+∠D,而∠2=∠B+∠E,则∠1=∠B+∠E+∠D,于是有∠A+∠B+∠C+∠D+∠E=180°;
(2)三角形外角性质得到∠1=∠C+∠E,∠2=∠B+∠D,再利用平角的定义得到∠1+∠CAD+∠2=180°,从而得到∠CAD+∠B+∠C+∠D+∠E=180°;
(3)由点D为AB的中点得到AD=BD,而∠ADF=∠BDC,DF=CD,根据三角形全等的判定方法得到△ADF≌△BDC,则∠1=∠DBC,同理可得△AGE≌△CBE,则∠2=∠ECB,根据三角形内角和定理得到∠ABC+∠ACB+∠BAC=180°,即∠1+∠2+∠BAC=180°,所以F、A、G三点在一条直线上.
点评:本题考查了三角形内角和定理:三角形内角和为180°.也考查了三角形外角性质以及全等三角形的判定与性质.

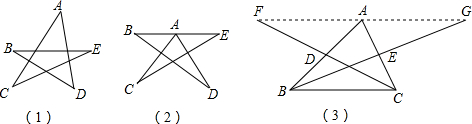
 180°;
180°;

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案