
如图中的△
ABC是等腰直角三角形,BC是斜边,P为△ABC内一点,将△ABP绕点A逆时针旋转后与△AC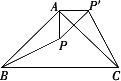
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:


查看答案和解析>>
科目:初中数学 来源: 题型:


查看答案和解析>>
科目:初中数学 来源:新课程同步练习 数学 八年级上册 题型:022
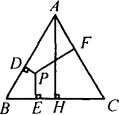
如图中,△ABC是等边三角形,点P是三角形内任一点,PD⊥AB于D,PE⊥BC于E,PF⊥AC于F,PH是BC边的高,且AH=h,则PD+PE十PF=________.(用h的代数或1表示.)
查看答案和解析>>
科目:初中数学 来源:三点一测丛书八年级数学上 题型:022
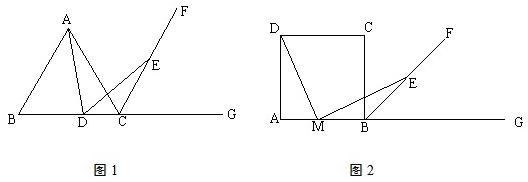
如图中,△ABC是等边三角形,D是BC上一点,△ABD经过旋转后到达△ACE的位置,旋转中心是点________,旋转了________度,若M是AB的中点,则经过上述旋转后,点M转到了________,BD=________,AD=________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com