
【题目】王浩同学用木板制作一个带有卡槽的三角形手机架,如图1所示.已知AC=20cm,BC=18cm,∠ACB=50°,王浩的手机长度为17cm,宽为8cm,王浩同学能否将手机放入卡槽AB内?请说明你的理由.(提示:sin50°≈0.8,cos50°≈0.6,tan50°≈1.2)
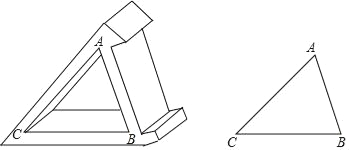
【答案】.能.
【解析】
试题
由题意可知,手机能不能放入卡槽AB内可以通过线段AB的长与手机的长17cm的比较来判断. 因此,本题就转化为如何求解线段AB的长. 分析已知条件可知,通过作△ABC的边BC上的高AD,可以利用已知条件中∠ACB的度数与边AC的长求解Rt△ADC,进而通过勾股定理得到线段AB的长.
试题解析:
王浩同学能将手机放入卡槽AB内. 理由如下.
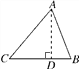
如图,过点A作AD⊥BC,垂足为D.
∵∠ACB=50°,AC=20cm,
∴在Rt△ADC中,
![]() (cm),
(cm),
![]() (cm),
(cm),
∵BC=18cm,
∴BD=BC-CD≈18-12=6(cm),
∴在Rt△ADB中,![]() (cm).
(cm).
∵![]() ,
,![]() ,
,
又∵![]() ,
,
∴AB>17,即卡槽AB的长度大于手机的长,
∴王浩同学能将手机放入卡槽AB内.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,正方形OABC的边长为4,顶点A,C分别在x轴、y轴的正半轴上,抛物线y=-![]() x2+bx+c经过点B,C两点,点D为抛物线的顶点,连接AC,BD,CD.
x2+bx+c经过点B,C两点,点D为抛物线的顶点,连接AC,BD,CD.
(1)求此抛物线的解析式;
(2)求此抛物线顶点D的坐标和四边形ABDC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
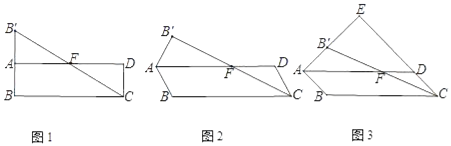
【题目】在ABCD中,点B关于AD的对称点为B′,连接AB′,CB′,CB′交AD于F点.
(1)如图1,∠ABC=90°,求证:F为CB′的中点;
(2)小宇通过观察、实验、提出猜想:如图2,在点B绕点A旋转的过程中,点F始终为CB′的中点.小宇把这个猜想与同学们进行交流,通过讨论,形成了证明该猜想的几种想法:
想法1:过点B′作B′G∥CD交AD于G点,只需证三角形全等;
想法2:连接BB′交AD于H点,只需证H为BB′的中点;
想法3:连接BB′,BF,只需证∠B′BC=90°.
…
请你参考上面的想法,证明F为CB′的中点.(一种方法即可)
(3)如图3,当∠ABC=135°时,AB′,CD的延长线相交于点E,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
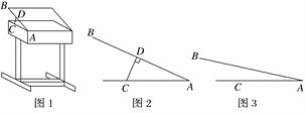
【题目】某课桌生产厂家研究发现,倾斜12°~24°的桌面有利于学生保持躯体自然姿势.根据这一研究,厂家决定将水平桌面做成可调节角度的桌面.新桌面的设计图如图1,AB可绕点A旋转,在点C处安装一根可旋转的支撑臂CD,AC=30 cm.
(1)如图2,当∠BAC=24°时,CD⊥AB,求支撑臂CD的长;
(2)如图3,当∠BAC=12°时,求AD的长.(结果保留根号)
(参考数据:sin 24°≈0.40,cos 24°≈0.91,tan 24°≈0.46,sin 12°≈0.20)
查看答案和解析>>
科目:初中数学 来源: 题型:
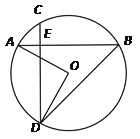
【题目】如图,在⊙O中,弦AB=弦CD,AB⊥CD于点E,且AE<EB,CE<ED,连结AO,DO,BD.
(1)求证:EB=ED.
(2)若AO=6,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次测量活动中,同学们要测量某公园的码头A与他正东方向的亭子B之间的距离,如图他们选择了与码头A、亭子B在同一水平面上的点P在点P处测得码头A位于点P北偏西方向30°方向,亭子B位于点P北偏东43°方向;又测得P与码头A之间的距离为200米,请你运用以上数据求出A与B的距离.
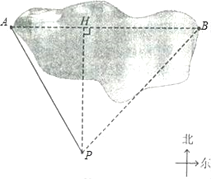
查看答案和解析>>
科目:初中数学 来源: 题型:
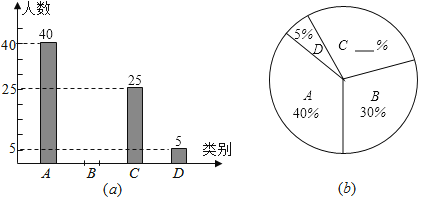
【题目】为了了解某区2018年初中毕业生毕业后的去向,某区教育部门对部分初三学生进行了抽样调查,就初三学生的四种去向(A,读普通高中;B,读职业高中;C,直接进入社会就业;D,其它)进行数据统计,并绘制了两幅不完整的统计图(a)、(b).请问:
(1)此次共调查了多少名初中毕业生?
(2)将两幅统计图中不完整的部分补充完整;
(3)若某区2018年初三毕业生共有3500人,请估计2019年初三毕业生中读普通高中的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
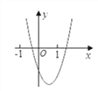
【题目】二次函数y=ax2+bx+c的图象如图,则一次函数y=bx+b2﹣4ac与反比例函数y=![]() 在同一坐标系内的图象大致为( )
在同一坐标系内的图象大致为( )
A.  B.
B.  C.
C. 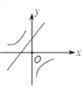 D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=2x+4与反比例函数y=![]() 的图象相交于A(-3,a)和B两点.
的图象相交于A(-3,a)和B两点.
(1)求k的值;
(2)直线y=m(m>0)与直线AB相交于点M,与反比例函数的图象相交于点N.若MN=4,求m的值;
(3)直接写出不等式![]() >x的解集.
>x的解集.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com