
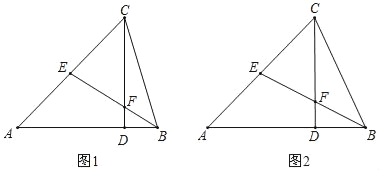
【题目】如图,△ABC中,∠A=45°,过点C作CD⊥AB于点D,E为AC的中点,连接EB,交CD于点F.
(1)如图1,若∠EBA=30°,EB=2,求AE的长:
(2)如图2,若F恰好为EB的中点,求证:CF=DF+![]() AD.
AD.
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:
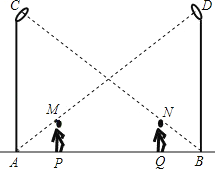
【题目】如图,王华同学在晚上由路灯AC走向路灯BD,当他走到点P时,发现身后他影子的顶部刚好接触到路灯AC的底部,当他向前再步行12m到达Q点时,发现身前他影子的顶部刚好接触到路灯BD的底部.已知王华同学的身高是1.6m,两个路灯的高度都是9.6m.
(1)求两个路灯之间的距离;
(2)当王华同学走到路灯BD处时,他在路灯AC下的影子长是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,直径AB垂直弦CD于E,过点A作∠DAF=∠DAB,过点D作AF的垂线,垂足为F,交AB的延长线于点P,连接CO并延长交⊙O于点G,连接EG.
(1)求证:DF是⊙O的切线;
(2)若AD=DP,OB=3,求![]() 的长度;
的长度;
(3)若DE=4,AE=8,求线段EG的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题错误的是( )
A. 如果y与x成反比例关系,那么x也与y成反比例关系
B. 如果y与z成反比例关系,z与x成正比例关系,且x≠0,那么y与x成反比例关系
C. 如果y与z成正比例关系,z与x成反比例关系,且x≠0,那么y与x成反比例关系
D. 如果y与z成反比例关系,z与x成反比例关系,那么y与x成反比例关系
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠B=90°,AB=12,BC=24,动点P从点A开始沿边AB向终点B以每秒2个单位长度的速度移动,动点Q从点B开始沿边BC以每秒4个单位长度的速度向终点C移动,如果点P、Q分别从点A、B同时出发,那么△PBQ的面积S随出发时间t(s)如何变化?写出函数关系式及t的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
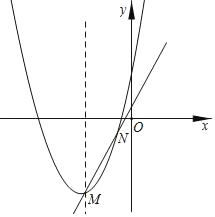
【题目】如图,已知抛物线y=x2+px+q的对称轴为直线x=﹣2,过其顶点M的一条直线y=kx+b与该抛物线的另一个交点为N(﹣1,﹣1).若要在y轴上找一点P,使得PM+PN最小,则点P的坐标为( ).
A. (0,﹣2) B. (0,﹣![]() ) C. (0,﹣
) C. (0,﹣![]() ) D. (0,﹣
) D. (0,﹣![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
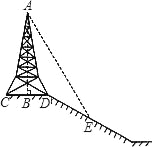
【题目】如图,在斜坡的顶部有一铁塔AB,B是CD的中点,CD是水平的,在阳光的照射下,塔影DE留在坡面上.已知铁塔底座宽CD=12 m,塔影长DE=18 m,小明和小华的身高都是1.6m,同一时刻,小明站在点E处,影子在坡面上,小华站在平地上,影子也在平地上,两人的影长分别为2m和1m,那么塔高AB为( )
A. 24m B. 22m C. 20m D. 18m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=x2+(a﹣2)x+3的图象与一次函数y=x(1≤x≤2)的图象有且仅有一个交点,则实数a的取值范围是( )
A. a=3±2![]() B. ﹣1≤a<2
B. ﹣1≤a<2
C. a=3![]() 或﹣
或﹣![]() ≤a<2 D. a=3﹣2
≤a<2 D. a=3﹣2![]() 或﹣1≤a<﹣
或﹣1≤a<﹣![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com