练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知直线y=kx+b经过点A（5，0），B（1，4）．

    （1）求直线AB的解析式；

    （2）若直线y=2x﹣4与直线AB相交于点C，求点C的坐标；

    （3）根据图象，写出关于x的不等式2x﹣4＞kx+b的解集．

    【答案】（1）y=-x+5；（2）点C（3，2）；（3）x＞3．

    【解析】试题分析：（1）利用待定系数法把点A（5，0），B（1，4）代入y=kx+b可得关于k、b得方程组，再解方程组即可；

    （2）联立两个函数解析式，再解方程组即可；

    （3）根据C点坐标可直接得到答案．

    试题解析：（1）∵直线y=kx+b经过点A（5，0），B（1，4），

    ∴，

    解得，

    ∴直线AB的解析式为：y=-x+5；

    （2）∵若直线y=2x-4与直线AB相交于点C，

    ∴．

    解得，

    ∴点C（3，2）；

    （3）根据图象可得x＞3．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

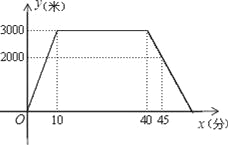
    【题目】小敏上午8：00从家里出发，骑车去一家超市购物，然后从这家超市返回家中．小敏离家的路程y（米）和所经过的时间x（分）之间的函数图象如图所示．请根据图象回答下列问题：

    （1）小敏去超市途中的速度是多少？在超市逗留了多少时间？

    （2）小敏几点几分返回到家？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，小红将一张直角梯形纸片沿虚线剪开，得到矩形和三角形两张纸片，测得AB=15，AD=12．在进行如下操作时遇到了下面的几个问题，请你帮助解决．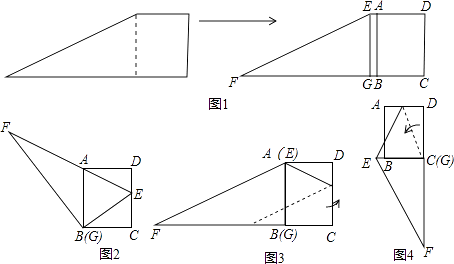

    （1）将△EFG的顶点G移到矩形的顶点B处，再将三角形绕点B顺时针旋转使E点落在CD边上，此时，EF恰好经过点A（如图2）求FB的长度；
    （2）在（1）的条件下，小红想用△EFG包裹矩形ABCD，她想了两种包裹的方法如图3、图4，请问哪种包裹纸片的方法使得未包裹住的面积大？（纸片厚度忽略不计）请你通过计算说服小红．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，△ABD，△ACE都是等边三角形，

    （1）求证：△ABE≌△ADC；

    （2）若∠ACD=15°，求∠AEB的度数；

    （3）如图2，当△ABD与△ACE的位置发生变化，使C、E、D三点在一条直线上，求证：AC∥BE．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，△ABD，△ACE都是等边三角形，

    （1）求证：△ABE≌△ADC；

    （2）若∠ACD=15°，求∠AEB的度数；

    （3）如图2，当△ABD与△ACE的位置发生变化，使C、E、D三点在一条直线上，求证：AC∥BE．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：如图，ABCD中，CD=CB=2，∠C=60°，点E是CD边上自D向C的动点（点E运动到点C停止运动），连结AE，以AE为一边作等边△AEP，连结DP．
    （1）求证：△ABE≌△ADP；
    （2）点P随点E的运动而运动，请直接写出点P的运动路径长 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，一艘巡逻艇航行至海面B处时，得知正北方向上距B处20海里的C处有一渔船发生故障，就立即指挥港口A处的救援艇前往C处营救．已知C处位于A处的北偏东45°的方向上，港口A位于B的北偏西30°的方向上．求A、C之间的距离．（结果精确到0.1海里，参考数据 ≈1.41， ≈1.73）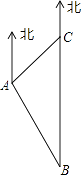

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】二次函数y=ax2+bx+c的部分图象如图所示，则下列正确的说法有（ ）
    ①点P（ac，b）在第二象限；
    ②x＞1时y随x的增大而增大；
    ③b2﹣4ac＞0；
    ④关于x的一元二次方程ax2+bx+c=0解为x1=﹣1，x2=3；
    ⑤关于x的不等式ax2+bx+c＞0 的解集为0＜x＜3．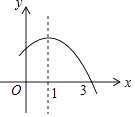

    A.2个
    B.3个
    C.4个
    D.5个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】解不等式（组）

    （Ⅰ）解不等式5x﹣2≥3（x+1），并把它的解集在数轴上表示出来．

    （Ⅱ）解不等式组

    请结合题意填空，完成本题的解答．

    解不等式①，得　 　；

    解不等式②，得　 　；

    把不等式①和②的解集在数轴上表示出来：

    原不等式组的解集为　 　．

    查看答案和解析>>

    同步练习册答案