
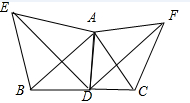
 如图,△ABC中,∠BAC=90°,AD⊥BC于点D,△ABE和△ACF都是等边三角形,若AD:BC=12:25,且AB>AC,求:
如图,△ABC中,∠BAC=90°,AD⊥BC于点D,△ABE和△ACF都是等边三角形,若AD:BC=12:25,且AB>AC,求:| S△DBE |
| S△DAF |
| S△DBE |
| S△DAF |
| DB |
| DA |

| BD |
| AD |
| AB |
| AC |
| BD |
| AD |
| BE |
| AF |
| S△DBE |
| S△DAF |
| DB |
| DA |
| AD |
| BC |
| 12 |
| 25 |
| BD |
| AD |
| AB |
| CA |
| S△DBE |
| S△DAF |
| DB |
| DA |
| 16 |
| 12 |
| 16 |
| 9 |


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:
 在边长为a的正方形ABCD内接一个正方形EFGH,设AE=x,正方形EFGH的面积为y.
在边长为a的正方形ABCD内接一个正方形EFGH,设AE=x,正方形EFGH的面积为y.查看答案和解析>>
科目:初中数学 来源: 题型:
| 10 |
| 3 |
| 15 |
| 7 |
查看答案和解析>>
科目:初中数学 来源: 题型:
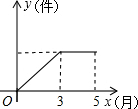 某产品前5个月生产总量y(件)与生产时间x(月)的关系如图所示,对于生产总量下列说法正确的是( )
某产品前5个月生产总量y(件)与生产时间x(月)的关系如图所示,对于生产总量下列说法正确的是( )| A、1至3月每月生产量不变,4,5两月停止生产 |
| B、1至3月每月生产量不变,4,5两月与3月份生产量持平 |
| C、1至3月每月生产量逐渐增加,4,5两月停止生产 |
| D、1至3月每月生产量逐渐增加,4,5两月与3月份生产量持平 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
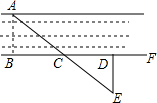 如图,要测量河岸相对两点A,B的距离,可以从AB的垂线BF上取两点C,D.使BC=CD,过D作DE⊥BF,且A,C,E三点在一直线上,若测得DE=30米,即AB=
如图,要测量河岸相对两点A,B的距离,可以从AB的垂线BF上取两点C,D.使BC=CD,过D作DE⊥BF,且A,C,E三点在一直线上,若测得DE=30米,即AB=查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com