
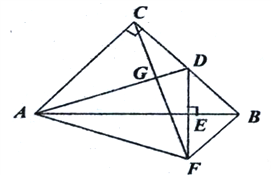
【题目】如图,在等腰Rt△ABC中,∠ACB=90![]() ,D为BC边上的中点,DE⊥AB,垂足为点E,过点B作BF∥AC交DE的延长线于点F,连接CF.
,D为BC边上的中点,DE⊥AB,垂足为点E,过点B作BF∥AC交DE的延长线于点F,连接CF.
(1)求证:AD⊥CF;
(2)连接AF,试判断△ACF的形状,并说明理由.

【答案】(1) 答案见解析;(2) 答案见解析
【解析】试题分析:
(1)由已知条件证:∠BDE=∠BFE=45°,从而可得:BF=BD,结合点D是CB的中点,可得BF=BD=CD;然后结合已知条件证:△ACD≌△CBF,从而可得:∠CAD=∠BCF,结合∠CAD+∠CDA=90![]() ,可得∠BCF+∠CDA=90
,可得∠BCF+∠CDA=90![]() ,这样就可得:∠AGC=90
,这样就可得:∠AGC=90![]() ,从而可得:AD⊥CF;
,从而可得:AD⊥CF;
(2)由(1)中BF=BD结合DE⊥AB可证:AB垂直平分DF,由此可得:AD=AF;由△ACD≌△CBF可得:AD=CF;两者结合可得:AF=CF,因此△ACF是等腰三角形.
试题解析:
(1)∵在等腰Rt△ABC中,∠ACB=90![]() ,
,
∴∠CBA=45![]() ,AC=BC .
,AC=BC .
又∵BF//AC, ∠ACB=90![]() ,
,
∴∠FBC=90![]() ,
,
∴∠FBE=45![]() .
.
又∵DE⊥AB,
∴∠BFE=45°,∠BDE=45°,
∴∠BFE=∠BDE,
∴BF=BD ,
∵D为BC的中点,
∴BD=CD,
∴ BF=CD.
在△ACD和△CBF中, 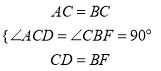 ,
,
∴ △ACD≌△CBF,
∴∠CAD=∠BCF,
又∵ ∠CAD+∠CDA=90![]() ,
,
∴∠BCF+∠CDA=90![]() ,
,
∴∠AGC=90![]() ,即AD⊥CF .
,即AD⊥CF .
(2)△ACF是等腰三角形,理由如下:
由(1)可知:△ACD≌△CBF;BD=BF,DE![]() AB,
AB,
∴CF=AD;DE=FE,
∴AB垂直平分DF,
∴AD=AF,
∴AF=CF ,
∴△ACF是等腰三角形.


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形OABC的顶点A、C的坐标分别为(10,0),(0,4),点D是OA的中点,点P在BC上运动,当△ODP是腰长为5的等腰三角形时,点P的坐标为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,A(2,0)、B(0,3),过点B作直线l∥x轴,点P(a,3)是直线上的动点,以AP为边在AP右侧作等腰RtAPQ,∠APQ=90°,直线AQ交y轴于点C.
(1)当a=![]() 时,求点Q的坐标;
时,求点Q的坐标;
(2)当PA+PO最小时,求a.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了追求更合适的出行体验,利用网络呼叫专车的打车方式受到大众欢迎.据了解在非高峰期时,某种专车所收取的费用![]() (元)与行驶里程
(元)与行驶里程![]()
![]() 的函数关系如图所示,请根据图象解答下列问题:
的函数关系如图所示,请根据图象解答下列问题:
(![]() )求
)求![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
(![]() )若专车低还行驶(时速
)若专车低还行驶(时速![]() ),每分钟另加
),每分钟另加![]() 元的低速费(不足
元的低速费(不足![]() 分钟的部分按
分钟的部分按![]() 分钟计算).某乘客有一次在非高峰期乘坐专车,途中低速行驶了
分钟计算).某乘客有一次在非高峰期乘坐专车,途中低速行驶了![]() 分钟,共付费
分钟,共付费![]() 元,求这位乘客坐专车的行驶里程.
元,求这位乘客坐专车的行驶里程.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文印店,一次性复印收费![]() (元)与复印面数(8开纸)
(元)与复印面数(8开纸) ![]() (面)的函数关系如图所示:
(面)的函数关系如图所示:
(1)从图象中可看出:复印超过50面的部分每面收费 元,复印200面平均每面收费 元;
(2)两同学各需要复印都不多于50面的资料,他们合起来去该店复印,结果比各自独去复印两人共节省2元钱,问其中一位同学所需复印的面数不能少于多少面?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图8,四边形ABEG、GEFH、HFCD都是边长为1的正方形.
(1)求证:△AEF∽△CEA;
(2)求证:∠AFB+∠ACB=45°.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角墙角AOB(OA⊥OB,且OA、OB长度不限)中,要砌20m长的墙,与直角墙角AOB围成地面为矩形的储仓,且地面矩形AOBC的面积为96m2.
(1)求地面矩形AOBC的长;
(2)有规格为0.80×0.80和1.00×1.00(单位:m)的地板砖单价分别为55元/块和80元/块,若只选其中一种地板砖都恰好能铺满储仓的矩形地面(不计缝隙),用哪一种规格的地板砖费用较少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】尺规作图:某学校正在进行校园环境的改造工程设计,准备在校内一块四边形花坛内栽上一棵桂花树.如图,要求桂花树的位置(视为点P),到花坛的两边AB、BC的距离相等,并且点P到点A、D的距离也相等.请用尺规作图作出栽种桂花树的位置点P(不写作法,保留作图痕迹).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】多项式 m2-4n2 与 m2-4mn+4n2 的公因式是( )
A. (m+2n)(m-2n) B. m+2n C. m-2n D. (m+2n)(m-2n)2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com