
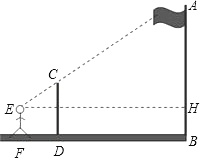
【题目】九年级(1)班课外活动小组利用标杆测量学校旗杆的高度,已知标杆高度CD=3m,标杆与旗杆的水平距离BD=15m,人的眼睛与地面的高度EF=1.6m,人与标杆CD的水平距离DF=2m,求旗杆AB的高度.
 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=a![]() -4ax与x轴交于A,B两点(A在B的左侧).
-4ax与x轴交于A,B两点(A在B的左侧).
(1)求点A,B的坐标;
(2)已知点C(2,1),P(1,-![]() a),点Q在直线PC上,且Q点的横坐标为4.
a),点Q在直线PC上,且Q点的横坐标为4.
①求Q点的纵坐标(用含a的式子表示);
②若抛物线与线段PQ恰有一个公共点,结合函数图象,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在初中阶段的函数学习中我们经历了“确定函数的表达,利用函数图象研究其性质﹣﹣运用函数解决问题”的学习过程,在画函数图象时,我们通过描点或平移的方法画出了所学的函数图象.已知函数y=2![]() ﹣b的定义域为x≥﹣3,且当x=0时y=2
﹣b的定义域为x≥﹣3,且当x=0时y=2![]() ﹣2由此,请根据学习函数的经验,对函数y=2
﹣2由此,请根据学习函数的经验,对函数y=2![]() ﹣b的图象与性质进行如下探究:
﹣b的图象与性质进行如下探究:
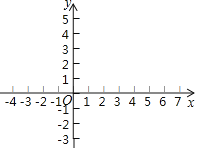
(1)函数的解析式为: ;
(2)在给定的平面直角坐标系xOy中,画出该函数的图象并写出该函数的一条性质: ;
(3)结合你所画的函数图象与y=x+1的图象,直接写出不等式2![]() ﹣b≤x+1的解集.
﹣b≤x+1的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题发现:
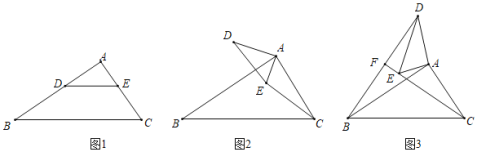
(1)如图1,在Rt△ABC中,∠A=90°,AB=kAC(k>1),D是AB上一点,DE∥BC,则BD,EC的数量关系为 .
类比探究
(2)如图2,将△AED绕着点A顺时针旋转,旋转角为a(0°<a<90°),连接CE,BD,请问(1)中BD,EC的数量关系还成立吗?说明理由
拓展延伸:
(3)如图3,在(2)的条件下,将△AED绕点A继续旋转,旋转角为a(a>90°).直线BD,CE交于F点,若AC=1,AB=![]() ,则当∠ACE=15°时,BFCF的值为_____.
,则当∠ACE=15°时,BFCF的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
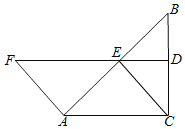
【题目】如图,在△ABC中,∠ACB=90°,BC的垂直平分线DE交BC于D,交AB于E,点F在DE的延长线上,且AF=CE=AE.
(1)求证:四边形ACEF是平行四边形;
(2)当∠B=30°时,试猜想四边形ACEF是什么图形,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某一时刻,小宁站在斜坡AC上的A处,小李在大楼FD的楼顶F处,此时小宁望小李的仰角为18.43°.5秒后,小宁沿斜坡AC前进到达C处,小李从大楼F处下楼到大楼E处,此时小李望小宁的俯角为22.6°;然后小李继续下楼,小宁沿CD前往楼底D处,已知小宁的速度为5.2米/秒,大楼FD的高度为30米,斜坡AC的坡度为1:2.4,小李、小宁都保持匀速前进,若斜坡、大楼在同一平面内,小李、小宁的身高忽略不计,则当小李达到楼底D处时,小宁距离D处的距离为( )米.
(已知:tan18.43°≈![]() ,sin18.43°≈
,sin18.43°≈![]() ,cos22.6°≈
,cos22.6°≈![]() ,tan22.6≈
,tan22.6≈![]() )
)

A.10B.15.6C.20.4D.26
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个四位数,若首位和末位都是1,称这样的数为“首尾双一数”,例如:1231,1581,1941等都是“首尾双一数”.
(1)证明:一个“首尾双一数”与它去掉首位和末位后得到的两位数的3倍的差能被7整除;
(2)给定一个“首尾双一数”n,记D(n)=![]() ,求满足D(n)是完全平方数,且n的所有位数上的数字之和为偶数的所有n.
,求满足D(n)是完全平方数,且n的所有位数上的数字之和为偶数的所有n.
查看答案和解析>>
科目:初中数学 来源: 题型:
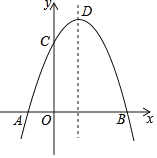
【题目】如图,抛物线y=﹣x2+2x+m交x轴于点A(a,0)和B(b,0),交y轴于点C,抛物线的顶点为D,下列四个结论:
①点C的坐标为(0,m);
②当m=0时,△ABD是等腰直角三角形;
③若a=﹣1,则b=4;
④抛物线上有两点P(x1,y1)和Q(x2,y2),若x1<1<x2,且x1+x2>2,则y1>y2.
其中结论正确的序号是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
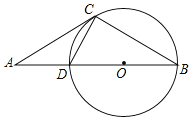
【题目】如图,点A是⊙O直径BD延长线上的一点,AC是⊙O的切线,C为切点.AD=CD,
(1)求证:AC=BC;
(2)若⊙O的半径为1,求△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com