
【题目】在初中阶段的函数学习中我们经历了“确定函数的表达,利用函数图象研究其性质﹣﹣运用函数解决问题”的学习过程,在画函数图象时,我们通过描点或平移的方法画出了所学的函数图象.已知函数y=2![]() ﹣b的定义域为x≥﹣3,且当x=0时y=2
﹣b的定义域为x≥﹣3,且当x=0时y=2![]() ﹣2由此,请根据学习函数的经验,对函数y=2
﹣2由此,请根据学习函数的经验,对函数y=2![]() ﹣b的图象与性质进行如下探究:
﹣b的图象与性质进行如下探究:
(1)函数的解析式为: ;
(2)在给定的平面直角坐标系xOy中,画出该函数的图象并写出该函数的一条性质: ;
(3)结合你所画的函数图象与y=x+1的图象,直接写出不等式2![]() ﹣b≤x+1的解集.
﹣b≤x+1的解集.
【答案】(1)y=2![]() ﹣2;(2)当x≥﹣3时,y随x的增大而增大;(3)x≥1
﹣2;(2)当x≥﹣3时,y随x的增大而增大;(3)x≥1
【解析】
(1)根据在函数y=y=2![]() ﹣b中,根据函数y=2
﹣b中,根据函数y=2![]() ﹣b的定义域为x≥﹣3,当x=0时y=2
﹣b的定义域为x≥﹣3,当x=0时y=2![]() ﹣2,可以求得该函数的表达式;
﹣2,可以求得该函数的表达式;
(2)根据(1)中的表达式可以画出该函数的图象并写出它的一条性质;
(3)根据图象可以直接写出所求不等式的解集.
(1)∵![]() ,
,
∴![]() ,
,
∵函数y=2![]() ﹣b的定义域为
﹣b的定义域为![]() ,
,
∴![]() ,
,
∵当![]() 时,
时,![]() ,
,
∴2![]() ﹣2=2
﹣2=2![]() ﹣b,
﹣b,
∴![]() ,
,
∴函数的解析式为:![]() ;
;
故答案为:y=2![]() ﹣2;
﹣2;
(2)
| -3 | -2 | -1 | 0 | 1 | 2 | 3 |
|
| -2 | 0 | 0.8 | 1.5 | 2 | 2.5 | 2.9 |
|
描点,按顺序连线该函数的图象如下图所示:
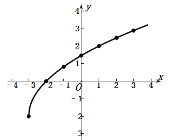
性质是当![]() 时,y随x的增大而增大;
时,y随x的增大而增大;
故答案为:当x≥﹣3时,y随x的增大而增大;
(3)如图,
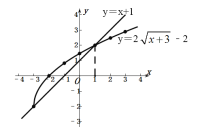
由函数图象可得,
不等式2![]() ﹣b≤x+1的解集是x≥1.
﹣b≤x+1的解集是x≥1.


科目:初中数学 来源: 题型:
【题目】图1是一种折叠门,由上下轨道和两扇长宽相等的活页门组成,整个活页门的右轴固定在门框
上,通过推动左侧活页门开关;图2是其俯视图简化示意图,已知轨道![]() ,两扇活页门的宽
,两扇活页门的宽![]() ,点
,点![]() 固定,当点
固定,当点![]() 在
在![]() 上左右运动时,
上左右运动时,![]() 与
与![]() 的长度不变(所有结果保留小数点后一位).
的长度不变(所有结果保留小数点后一位).
(1)若![]() ,求
,求![]() 的长;
的长;
(2)当点![]() 从点
从点![]() 向右运动60
向右运动60![]() 时,求点
时,求点![]() 在此过程中运动的路径长.
在此过程中运动的路径长.
(参考数据:sin50°≈0.77, cos50°≈0.64, tan50°≈1.19, π取3.14)

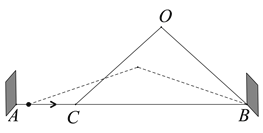
图1 图2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小亮一家在一湖泊中游玩,湖泊中有一孤岛,妈妈在孤岛P处观看小亮与爸爸在湖中划船(如图所示).小船从P处出发,沿北偏东60°方向划行200米到A处,接着向正南方向划行一段时间到B处.在B处小亮观测到妈妈所在的P处在北偏西37°的方向上,这时小亮与妈妈相距多少米(精确到1米)?
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)

查看答案和解析>>
科目:初中数学 来源: 题型:
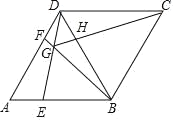
【题目】如图,在菱形![]() 中,
中,![]() ,点
,点![]() 分别是线段
分别是线段![]() 上的动点(不与端点重合),且
上的动点(不与端点重合),且![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() .给出如下几个结论:
.给出如下几个结论:
①![]()
②![]() 平分
平分![]() ;
;
③若![]() ,则
,则![]()
④![]()
其中正确的结论是_____________(填写所有正确结论的序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点P在函数y=![]() (x>0)的图象上从左向右运动,PA∥y轴,交函数y=﹣
(x>0)的图象上从左向右运动,PA∥y轴,交函数y=﹣![]() (x>0)的图象于点A,AB∥x轴交PO的延长线于点B,则△PAB的面积( )
(x>0)的图象于点A,AB∥x轴交PO的延长线于点B,则△PAB的面积( )
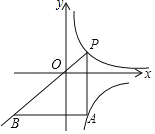
A.逐渐变大B.逐渐变小C.等于定值16D.等于定值24
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A在x轴正半轴上,点B在y轴正半轴上,O为坐标原点,OA=OB=1,过点O作OM1⊥AB于点M1;过点M1作M1A1⊥OA于点A1:过点A1作A1M2⊥AB于点M2;过点M2作M2A2⊥OA于点A2…以此类推,点M2019的坐标为_____.
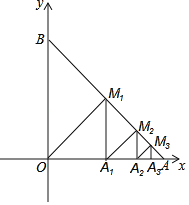
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在矩形ABCD中,AB<BC,点E为对角线AC上的一个动点,连接BE,DE,过E作EF⊥BC于F.设AE=x,图1中某条线段的长为y,若表示y与x的函数关系的图象大致如图2所示,则这条线段可能是图1中的( )
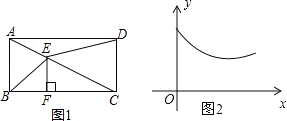
A.线段BEB.线段EFC.线段CED.线段DE
查看答案和解析>>
科目:初中数学 来源: 题型:
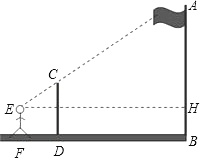
【题目】九年级(1)班课外活动小组利用标杆测量学校旗杆的高度,已知标杆高度CD=3m,标杆与旗杆的水平距离BD=15m,人的眼睛与地面的高度EF=1.6m,人与标杆CD的水平距离DF=2m,求旗杆AB的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线C1:y=ax2+bx+c向左平移1个单位长度,再向上平移4个单位长度得到抛物线C2:y=x2.

(1)直接写出抛物线C1的解析式 ;
(2)如图1,已知抛物线C1与x轴交于A,B两点,点A在点B的左侧,点P(![]() ,t)在抛物线C1上,QB⊥PB交抛物线于点Q.求点Q的坐标;
,t)在抛物线C1上,QB⊥PB交抛物线于点Q.求点Q的坐标;
(3)已知点E,M在抛物线C2上,EM∥x轴,点E在点M的左侧,过点M的直线MD与抛物线C2只有一个公共点(MD与y轴不平行),直线DE与抛物线交于另一点N.若线段NE=DE,设点M,N的横坐标分别为m,n,直接写出m和n的数量关系(用含m的式子表示n)为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com