
【题目】已知抛物线C1:y=ax2+bx+c向左平移1个单位长度,再向上平移4个单位长度得到抛物线C2:y=x2.

(1)直接写出抛物线C1的解析式 ;
(2)如图1,已知抛物线C1与x轴交于A,B两点,点A在点B的左侧,点P(![]() ,t)在抛物线C1上,QB⊥PB交抛物线于点Q.求点Q的坐标;
,t)在抛物线C1上,QB⊥PB交抛物线于点Q.求点Q的坐标;
(3)已知点E,M在抛物线C2上,EM∥x轴,点E在点M的左侧,过点M的直线MD与抛物线C2只有一个公共点(MD与y轴不平行),直线DE与抛物线交于另一点N.若线段NE=DE,设点M,N的横坐标分别为m,n,直接写出m和n的数量关系(用含m的式子表示n)为 .
【答案】(1)y=(x﹣1)2﹣4;(2)Q(﹣![]() ,
,![]() );(3)n=(1±2
);(3)n=(1±2![]() )m
)m
【解析】
(1)逆向考虑,抛物线C2平移到抛物线C1,即可求抛物线C1的解析式;
(2)求出A、B、P的点的坐标,设Q(t,t2-2t-3),过点P作PM⊥x轴交于点M,过点Q作QN⊥x轴交于点N,可以证明△BNQ∽△QMP,由相似可得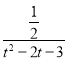 =
=![]() ,求出t即可;
,求出t即可;
(3)求出M、N、E点坐标,设MD的解析式为y=kx+b,将点M代入解析式可得y=kx+m2-km,再由直线MD与抛物线y=x2只有一个交点,联立方程kx+m2-km=x2,由判别式△=0可得k=2m,则直线MD为y=2mx-m2,在求出D点坐标代入MD的解析式即可求解.
(1)由已知可知,抛物线C2:y=x2向右平移1个单位长度,再向下平移4个单位长度得到抛物线C1:y=ax2+bx+c,
∴抛物线C1:y=(x﹣1)2﹣4,
故答案为y=(x﹣1)2﹣4;
(2)∵y=(x﹣1)2﹣4,
令y=0,(x﹣1)2﹣4=0,
解得x=3或x=﹣1,
∴A(﹣1,0),B(3,0),
∵点P(![]() ,t)在抛物线C1上,
,t)在抛物线C1上,
∴t=(![]() ﹣1)2﹣4,解得t=﹣
﹣1)2﹣4,解得t=﹣![]() ,
,
∴P(![]() ,﹣
,﹣![]() ),
),
设Q(t,t2﹣2t﹣3),
过点P作PM⊥x轴交于点M,过点Q作QN⊥x轴交于点N,
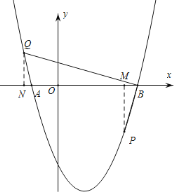
∵BQ⊥BP,
∴∠QBN+∠MBP=∠QBN+∠MQN=90°,
∴∠BQN=∠PBM,
∴△BNQ∽△QMP,
∴![]() =
=![]() ,
,
∴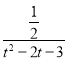 =
=![]() ,
,
∴t=﹣![]() 或t=3,
或t=3,
∵Q点在第二象限,
∴t=﹣![]() ,
,
∴Q(﹣![]() ,
,![]() );
);
(3)∵点M与N在y=x2上,
∴M(m,m2),N(n,n2)
∵EM∥x轴,
∴E(﹣m,m2),
设MD的解析式为y=kx+b,
∴m2=km+b,
∴b=m2﹣km,
∴y=kx+m2﹣km,
∵直线MD与抛物线y=x2只有一个交点,
∴kx+m2﹣km=x2,
∴△=k2﹣4(m2+km)=0,
∴k=2m,
∴直线MD的解析式为y=2mx﹣m2,
∵NE=DE,
∴D(﹣2m﹣n,2m2﹣n2),
∴2m2﹣n2=2m(﹣2m﹣n)﹣m2,
整理得,n2﹣2mn﹣7m2=0,
∴n=(1±2![]() )m,
)m,
故答案为n=(1±2![]() )m.
)m.


科目:初中数学 来源: 题型:
【题目】在初中阶段的函数学习中我们经历了“确定函数的表达,利用函数图象研究其性质﹣﹣运用函数解决问题”的学习过程,在画函数图象时,我们通过描点或平移的方法画出了所学的函数图象.已知函数y=2![]() ﹣b的定义域为x≥﹣3,且当x=0时y=2
﹣b的定义域为x≥﹣3,且当x=0时y=2![]() ﹣2由此,请根据学习函数的经验,对函数y=2
﹣2由此,请根据学习函数的经验,对函数y=2![]() ﹣b的图象与性质进行如下探究:
﹣b的图象与性质进行如下探究:
(1)函数的解析式为: ;
(2)在给定的平面直角坐标系xOy中,画出该函数的图象并写出该函数的一条性质: ;
(3)结合你所画的函数图象与y=x+1的图象,直接写出不等式2![]() ﹣b≤x+1的解集.
﹣b≤x+1的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个四位数,若首位和末位都是1,称这样的数为“首尾双一数”,例如:1231,1581,1941等都是“首尾双一数”.
(1)证明:一个“首尾双一数”与它去掉首位和末位后得到的两位数的3倍的差能被7整除;
(2)给定一个“首尾双一数”n,记D(n)=![]() ,求满足D(n)是完全平方数,且n的所有位数上的数字之和为偶数的所有n.
,求满足D(n)是完全平方数,且n的所有位数上的数字之和为偶数的所有n.
查看答案和解析>>
科目:初中数学 来源: 题型:
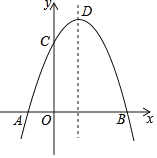
【题目】如图,抛物线y=﹣x2+2x+m交x轴于点A(a,0)和B(b,0),交y轴于点C,抛物线的顶点为D,下列四个结论:
①点C的坐标为(0,m);
②当m=0时,△ABD是等腰直角三角形;
③若a=﹣1,则b=4;
④抛物线上有两点P(x1,y1)和Q(x2,y2),若x1<1<x2,且x1+x2>2,则y1>y2.
其中结论正确的序号是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司共有![]() 三个部门,根据每个部门的员工人数和相应每人所创的年利润绘制成如下的统计表和扇形图.
三个部门,根据每个部门的员工人数和相应每人所创的年利润绘制成如下的统计表和扇形图.

各部门人数及每人所创年利润统计表
部门 | 员工人数 | 每人所创的年利润/万元 |
A | 5 | 10 |
B |
| 8 |
C |
| 5 |
(1)①在扇形图中,C部门所对应的圆心角的度数为___________;
②在统计表中,![]() ___________,
___________,![]() ___________;
___________;
(2)求这个公司平均每人所创年利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】文具店有三种品牌的6个笔记本,价格是4,5,7(单位:元)三种,从中随机拿出一个本,已知![]() (一次拿到7元本)
(一次拿到7元本)![]() .
.
(1)求这6个本价格的众数.
(2)若琪琪已拿走一个7元本,嘉嘉准备从剩余5个本中随机拿一个本.
①所剩的5个本价格的中位数与原来6个本价格的中位数是否相同?并简要说明理由;
②嘉嘉先随机拿出一个本后不放回,之后又随机从剩余的本中拿一个本,用列表法求嘉嘉两次都拿到7元本的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
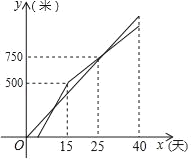
【题目】甲、乙两个工程队共同开凿一条隧道,甲队按一定的工作效率先施工,一段时间后,乙队从隧道的另一端按一定的工作效率加入施工,中途乙队调离一部分工人去完成其他任务,工作效率降低.当隧道气打通时,甲队工作了40天,设甲,乙两队各自开凿隧道的长度为y(米),甲队的工作时间为x(天),y与x之间的函数图象如图所示.
(1)求甲队的工作效率.
(2)求乙队调离一部分工人后y与x之间的函数关系式
(3)求这条隧道的总长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
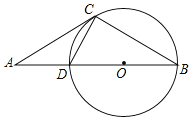
【题目】如图,点A是⊙O直径BD延长线上的一点,AC是⊙O的切线,C为切点.AD=CD,
(1)求证:AC=BC;
(2)若⊙O的半径为1,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠ABC=70°,以B为圆心,任意长为半径画弧交AB,BC于点E,F,再分别以点E,F为圆心、以大于![]() EF长为半径画弧,两弧交于点P,作射线BP交AC于点D,则∠BDC为( )度.
EF长为半径画弧,两弧交于点P,作射线BP交AC于点D,则∠BDC为( )度.
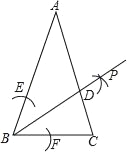
A. 65 B. 75 C. 80 D. 85
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com