
����Ŀ���ľߵ�������Ʒ�Ƶ�6���ʼDZ����۸���4��5��7����λ��Ԫ�����֣���������ó�һ��������֪![]() ��һ���õ�7Ԫ����
��һ���õ�7Ԫ����![]() ��
��
��1������6�����۸��������
��2��������������һ��7Ԫ�����μ�����ʣ��5�����������һ������
����ʣ��5�����۸����λ����ԭ��6�����۸����λ���Ƿ���ͬ������Ҫ˵�����ɣ�
�ڼμ�������ó�һ�����Żأ�֮���������ʣ��ı�����һ���������б�����μ����ζ��õ�7Ԫ���ĸ��ʣ�
���𰸡���1��������7����2������ͬ������⣻��![]()
��������
(1)�ɸ��ʹ�ʽ���7Ԫ���ĸ������������Ķ��弴�ɵó��𰸣�
(2)������λ���Ķ��弴�ɵó��𰸣�
�����б����ó����н�����μ����ζ��õ�7Ԫ���Ľ����6�����ɸ��ʹ�ʽ���ɵó��𰸣�
��:
��1����![]() ��һ���õ�7Ԫ����
��һ���õ�7Ԫ����![]() ��
��
��7Ԫ���ĸ���Ϊ6��![]() =4(��)�����մ�С�����˳������Ϊ4��5�� 7��7��7,7,
=4(��)�����մ�С�����˳������Ϊ4��5�� 7��7��7,7,
����6�����۸��������7.
��2������ͬ��
��ԭ��4��5��7��7��7��7������λ��Ϊ![]() ��
��
5���۸�Ϊ4��5��7��7��7����λ��Ϊ7��
��![]() ������ͬ.
������ͬ.
�ڼ�ͼ
��һ�� �ڶ��� | 4 | 5 | 7 | 7 | 7 |
4 |
|
|
|
| |
5 |
|
|
|
| |
7 |
|
|
|
| |
7 |
|
|
|
| |
7 |
|
|
|
|
��![]() �����ζ�Ϊ7��
�����ζ�Ϊ7��![]() .
.


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У���A��x���������ϣ���B��y���������ϣ�OΪ����ԭ�㣬OA��OB��1������O��OM1��AB�ڵ�M1������M1��M1A1��OA�ڵ�A1������A1��A1M2��AB�ڵ�M2������M2��M2A2��OA�ڵ�A2���Դ����ƣ���M2019������Ϊ_____��
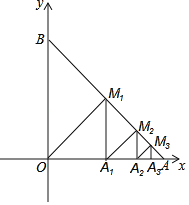
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ͬʱ�������ʵؾ��ȵ����ӣ��۲�����һ��ĵ������������ӵĵ�����ͬ�ĸ����ǣ� ��
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ƽ��ֱ������ϵ![]() �е�ͼ��M��N���������¶��壺�����PΪͼ��M������һ�㣬��QΪͼ��N������һ�㣬��ô���߶�PQ���ȵ���СֵΪͼ��M��N������������������ d��M��N������ͼ��M��N������������С�ڻ����1�����ͼ��M��N��Ϊ���ɼ�ͼ������
�е�ͼ��M��N���������¶��壺�����PΪͼ��M������һ�㣬��QΪͼ��N������һ�㣬��ô���߶�PQ���ȵ���СֵΪͼ��M��N������������������ d��M��N������ͼ��M��N������������С�ڻ����1�����ͼ��M��N��Ϊ���ɼ�ͼ������
��1������O�İ뾶Ϊ2ʱ��
�������A��0��1����B��3��4������ôd��A����O��=_______,d��B����O��= ________��
�����ֱ��![]() ���O��Ϊ���ɼ�ͼ��������b��ȡֵ��Χ��
���O��Ϊ���ɼ�ͼ��������b��ȡֵ��Χ��
��2����G��Բ��G��![]() ���ϣ��뾶Ϊ1��ֱ��
���ϣ��뾶Ϊ1��ֱ��![]() ��x�ύ�ڵ�C����y�ύ�ڵ�D�������G�͡�CDO��Ϊ���ɼ�ͼ������ֱ��д��Բ��G�ĺ�����m��ȡֵ��Χ��
��x�ύ�ڵ�C����y�ύ�ڵ�D�������G�͡�CDO��Ϊ���ɼ�ͼ������ֱ��д��Բ��G�ĺ�����m��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������C1��y��ax2+bx+c����ƽ��1����λ���ȣ�������ƽ��4����λ���ȵõ�������C2��y��x2��

��1��ֱ��д��������C1�Ľ���ʽ�� ����
��2����ͼ1����֪������C1��x�ύ��A��B���㣬��A�ڵ�B����࣬��P��![]() ��t����������C1�ϣ�QB��PB���������ڵ�Q�����Q�����ꣻ
��t����������C1�ϣ�QB��PB���������ڵ�Q�����Q�����ꣻ
��3����֪��E��M��������C2�ϣ�EM��x�ᣬ��E�ڵ�M����࣬����M��ֱ��MD��������C2ֻ��һ�������㣨MD��y�ƽ�У���ֱ��DE�������߽�����һ��N�����߶�NE��DE�����M��N�ĺ�����ֱ�Ϊm��n��ֱ��д��m��n��������ϵ���ú�m��ʽ�ӱ�ʾn��Ϊ�� ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������y����x2+3x+2��y�ύ�ڵ�A����B�������ߵĶ��㣬��C���A���������Ϲ��ڶԳ���ԳƵ������㣬��D��x�����˶������ı���ABCD�������Խ��ߵij���֮�͵���СֵΪ_____��
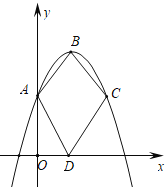
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����κ���![]() ��a��0����ͼ����x�ύ��A��B���㣬��y�ύ��C�㣬�ҶԳ���Ϊx=1����B����Ϊ����1��0������������ĸ����ۣ���2a+b=0����4a��2b��c��0����ac��0������y��0ʱ��x����1��x��2��������ȷ�ĸ�����
��a��0����ͼ����x�ύ��A��B���㣬��y�ύ��C�㣬�ҶԳ���Ϊx=1����B����Ϊ����1��0������������ĸ����ۣ���2a+b=0����4a��2b��c��0����ac��0������y��0ʱ��x����1��x��2��������ȷ�ĸ�����
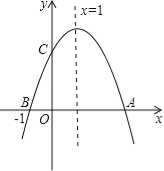
A.1B.2C.3D.4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У���ACB=90����AC=BC��P����ABC����һ�㣬����APB=��APC=135����
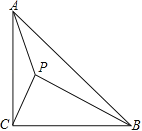
��1����֤����CPA�ס�APB��
��2������tan��PCB��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
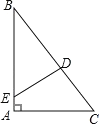
����Ŀ����ͼ����ij��˹ŵ�˱����У�����λ�ڵ� A �����ڵ� A ��������ĵ� B ����һ�ź����ڵ� A �������� C ����һ�ź����� BC ���м�ĵ� D ����һ���������е� C �ڵ� B ����ƫ�� 37�������ϣ�ѡ�ֽ����������������ƽ� 10cm ����� E ��ʱ����õ�D �ڵ�E �ı�ƫ��45�������ϣ����ʱ���������ľ����ж�Զ�����ο����ݣ�sin37���![]() ��cos37���
��cos37��� ![]() ��tan37���
��tan37���![]() ��
��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com