
【题目】如图,已知抛物线y=x2+bx+c经过点(0,﹣3),请你确定一个b的值,使该抛物线与x轴的一个交点在(1,0)和(3,0)之间.你确定的b的值是 . 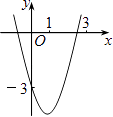
【答案】1(在﹣2<b<2范围内的任何一个数)
【解析】解:把(0,﹣3)代入抛物线的解析式得:c=﹣3,
∴y=x2+bx﹣3,
∵使该抛物线与x轴的一个交点在(1,0)和(3,0)之间,
∴把x=1代入y=x2+bx﹣3得:y=1+b﹣3<0
把x=3代入y=x2+bx﹣3得:y=9+3b﹣3>0,
∴﹣2<b<2,
即在﹣2<b<2范围内的任何一个数都符合,
所以答案是:1(在﹣2<b<2范围内的任何一个数).
【考点精析】认真审题,首先需要了解抛物线与坐标轴的交点(一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.).


 优加精卷系列答案
优加精卷系列答案科目:初中数学 来源: 题型:
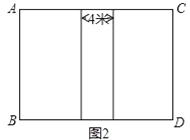
【题目】某校为学生开展拓展性课程,拟在一块长比宽多6米的长方形场地内建造由两个大棚组成的植物养殖区(如图1),要求两个大棚之间有间隔4米的路,设计方案如图2,已知每个大棚的周长为44米.
(1)求每个大棚的长和宽各是多少?
(2)现有两种大棚造价的方案,方案一是每平方米60元,超过100平方米优惠500元,方案二是每平方米70元,超过100平方米优惠总价的20%,试问选择哪种方案更优惠?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列方程的变形正确的是( )
A.由2x﹣3=4x,得:2x=4x﹣3
B.由7x﹣4=3﹣2x,得:7x+2x=3﹣4
C.由 ![]() x﹣
x﹣ ![]() =3x+4得﹣
=3x+4得﹣ ![]() ﹣4=3x+
﹣4=3x+ ![]() x
x
D.由3x﹣4=7x+5得:3x﹣7x=5+4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l和双曲线 ![]() 交于A,B两点,P是线段AB上的点(不与A,B重合),过点A,B,P分别向x轴作垂线,垂足分别为C,D,E,连接OA,OB,0P,设△AOC的面积为S1、△BOD的面积为S2、△POE的面积为S3 , 则( )
交于A,B两点,P是线段AB上的点(不与A,B重合),过点A,B,P分别向x轴作垂线,垂足分别为C,D,E,连接OA,OB,0P,设△AOC的面积为S1、△BOD的面积为S2、△POE的面积为S3 , 则( )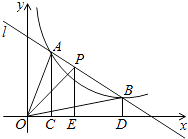
A.S1<S2<S3
B.S1>S2>S3
C.S1=S2>S3
D.S1=S2<S3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正五边形ABCDE中,直线![]() 过点B,且
过点B,且![]() ⊥ED,下列说法:①
⊥ED,下列说法:①![]() 是线段AC的垂直平分线;②∠BAC=36°;③正五边形ABCDE有五条对称轴.正确的有( ).
是线段AC的垂直平分线;②∠BAC=36°;③正五边形ABCDE有五条对称轴.正确的有( ).

A. ①②B. ①③C. ②③D. ①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
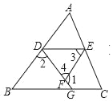
【题目】如图,已知∠1+∠2=180°,∠3=∠B,试判断DE与BC的位置关系,并对结论进行说理.
证明:DE∥BC.
理由如下:
∵∠1+∠2=180°(已知)
∠1+∠4=180°(平角定义)
∴∠2=∠4(同角的补角相等)
∴ ∥ ( )
∴∠3+ =180°( )
∵∠3=∠B(已知)
∴∠B+ =180°(等量代换)
∴ ∥ ( )
查看答案和解析>>
科目:初中数学 来源: 题型:
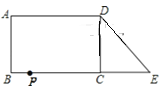
【题目】已知:如图,在长方形ABCD中,AB=4,AD=6.延长BC到点E,使CE=3,连接DE,动点P从点B出发,以每秒1个单位的速度沿BC﹣CD﹣DA向终点A运动,设点P的运动时间为t秒,当t的值为__________秒时.△ABP和△DCE全等.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com