
【题目】如图,正五边形ABCDE中,直线![]() 过点B,且
过点B,且![]() ⊥ED,下列说法:①
⊥ED,下列说法:①![]() 是线段AC的垂直平分线;②∠BAC=36°;③正五边形ABCDE有五条对称轴.正确的有( ).
是线段AC的垂直平分线;②∠BAC=36°;③正五边形ABCDE有五条对称轴.正确的有( ).

A. ①②B. ①③C. ②③D. ①②③
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案科目:初中数学 来源: 题型:
【题目】△ABC与△A'B'C'在平面直角坐标系中的位置如图所示
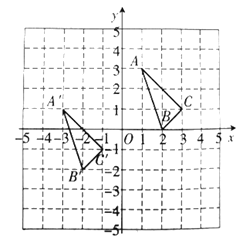
(1)分别写出下列各点的坐标:A_______ B_______ C_______
(2)△ABC由△A'B'C'经过怎样的平移得到?
(3)若点P(x,y)是△ABC内部点,则A'B'C' 内部的对应点P'的坐标为
(4)求△ABC的面积
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=x2+bx+c经过点(0,﹣3),请你确定一个b的值,使该抛物线与x轴的一个交点在(1,0)和(3,0)之间.你确定的b的值是 . 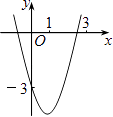
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校计划购买篮球、排球共20个,购买2个篮球,3个排球,共需花费190元;购买3个篮球的费用与购买5个排球的费用相同。
(1)篮球和排球的单价各是多少元?
(2)若购买篮球不少于8个,所需费用总额不超过800元.请你求出满足要求的所有购买方案,并直接写出其中最省钱的购买方案
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆轿车和一辆货车同时从甲地出发,已知轿车的速度比货车的速度每小时快20千米,当轿车行驶到距甲地360千米的丙地时,货年恰好行驶到距离甲地300千米的乙地,问轿车与货车的速度分别是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程kx2+(2k+1)x+2=0.
(1)求证:无论k取任何实数时,方程总有实数根;
(2)当抛物线y=kx2+(2k+1)x+2图象与x轴两个交点的横坐标均为整数,且k为正整数时,若P(a,y1),Q(1,y2)是此抛物线上的两点,且y1>y2 , 请结合函数图象确定实数a的取值范围;
(3)已知抛物线y=kx2+(2k+1)x+2恒过定点,求出定点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级甲、乙两班分别选5名同学参加“学雷锋读书活动”演讲比赛,其预赛成绩如图:

(1)根据上图求出下表所缺数据;
平均数 | 中位数 | 众数 | 方差 | |
甲班 | 8.5 | 8.5 | ||
乙班 | 8 | 10 | 1.6 |
(2)根据上表中的平均数、中位数和方差你认为哪班的成绩较好?并说明你的理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com