
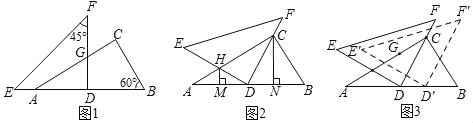
����Ŀ����һ�����dz߰�ͼ1�ڷţ�����ֱ�����dzߵ�ֱ�DZ�DFǡ�ô�ֱƽ��AB����AC�ཻ�ڵ�G��![]() ��
��
��1����GC�ij���
��2����ͼ2������DEF�Ƶ�D˳ʱ����ת��ʹֱ�DZ�DF������C����һֱ�DZ�DE��AC�ཻ�ڵ�H���ֱ��H��C��AB�Ĵ��ߣ�����ֱ�ΪM��N��ͨ���۲죬����MD��ND��������ϵ������֤��IJ��룮
��3���ڣ�2���������£�����DEF��DB����ƽ�Ƶõ���D��E��F�䣬��D��E��ǡ�þ�����1���еĵ�Gʱ����ֱ��д��DD��ij��ȣ�
���𰸡���1��2����2��DM=DN����3��![]()
��������
��1����ֱ�����������AC��AG���ɽ�����⣻
��2����ֱ��������б���ϵ����ߵ���б�ߵ�һ�룬�õ�CD=BD=AD�����ɡ�B=60�㣬�õ���BDCΪ�ȱ������Σ��Ӷ�����֤����HDA=30�㣬��һ���õ� AH=HD���ɵ��������ε����ʵõ�MD=AM��ND=NB�����ɵõ����ۣ�
��3����ͼ3�У���GK��DE��AB��K�����AK��ֵ���ɽ�����⣮
��1����ͼ1��
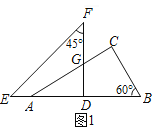
��Rt��ABC�У���BC=2![]() ����B=60�㣬��AC=BCtan60��=6��AB=2BC=4
����B=60�㣬��AC=BCtan60��=6��AB=2BC=4![]() ��
��
��DF���߶�AB�Ĵ�ֱƽ���ߣ���AD=BD=2![]() ��
��
��Rt��ADG��AG![]() 4����CG=AC=AG=6��4=2��
4����CG=AC=AG=6��4=2��
��2����ͼ2�У����ۣ�DM=DN��
���ɣ��ߡ�ABCΪֱ�������Σ�DΪб��AB���е㣬��CD=BD=AD��
�֡�B=60�㣬���BDCΪ�ȱ������Σ����CDB=60�㣮
�֡�EDF=90�㣬���HDA=30�㣮
�ߡ�A=90�㩁��B=30�㣬��AH=HD����HM��AD����MD=AM��
�ڵȱ������� BCD�У�CN��BD����ND=NB��
��AD=BD����MD=ND��
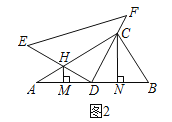
��3����ͼ3�У���GK��DE��AB��K��
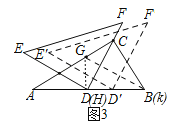
�ڡ�AGK�У�AG=GK=4����A=��GKD=30�㣬��GH��AB��H��
��AH=AGcos30��=2![]() ���ɵ�AK=2AH=4
���ɵ�AK=2AH=4![]() ����ʱK��B�غϣ���DD��=DB=2
����ʱK��B�غϣ���DD��=DB=2![]() ��
��


 �ƸԾ���Ȥζ����ϵ�д�
�ƸԾ���Ȥζ����ϵ�д� ����С����ҵ��ϵ�д�
����С����ҵ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ��AB����O��ֱ����C��D����O�ϵĵ㣬��OC��BD, AD�ֱ���BC��OC�ཻ�ڵ�E��F�������н��ۣ���AD��BD; �ڡ�AOC=��AEC; ��CBƽ�֡�ABD;��AF=DF; ��BD=2OF; �ޡ�CEF �ա�BED,����һ���������ǣ� ��
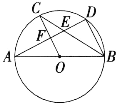
A. �� �� �� �� B. �� �� �� ��
C. �� �� �� �� D. �� �� �� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�κ���y=-x+4��ͼ���뷴��������y=![]() ��kΪ��������k��0����ͼ����A��1��a����B���㣮
��kΪ��������k��0����ͼ����A��1��a����B���㣮
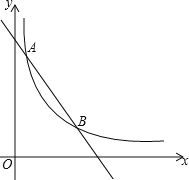
��1�����������ı���ʽ����B�����ꣻ
��2�����ͼ��ֱ��д������ʽ-x+4��![]() �Ľ⼯
�Ľ⼯
��3����x������һ��P��ʹPA+PB��ֵ��С�������������ĵ�P�����꼰��PAB�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��y=��4x+4��x�ᡢy��ֱ���A��B���㣬��ABΪ���ڵ�һ������������ABCD����������ABCD��x�Ḻ����ƽ��a����λ���Ⱥ�Cǡ������˫�����ڵ�һ���ķ�֧�ϣ���a��ֵ��_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��PA��PB�ǡ�O���������ߣ�A��B���е㣬AC�ǡ�O��ֱ������BAC��35�㣬���P�Ķ�����
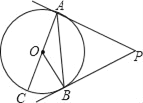
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������y��ax��a��y��![]() ��a��0����ͬһֱ������ϵ�е�ͼ������ǣ�������
��a��0����ͬһֱ������ϵ�е�ͼ������ǣ�������
A.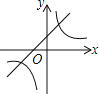 B.
B.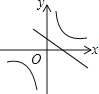
C.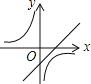 D.
D.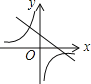
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڵ�����ABC�У�AB��AC��AD��BC������ΪD���� ADΪֱ������O����O�ֱ�AB��AC�� E��F��
��1����֤��BE��CF��
��2���� AD��EF�ཻ��G���� EF��8����O�İ뾶Ϊ5����DG�ij���
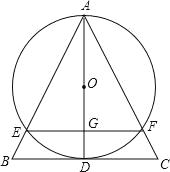
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
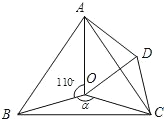
����Ŀ����ͼ���� O �ǵȱ���ABC ��һ�㣬��AOB��110�㣬��BOC��a������BOC �Ƶ� C ��˳ʱ�뷽����ת 60������ADC������ADC�ա�BOC������ OD��
��1����֤����COD �ǵȱ������Σ�
��2��������120��ʱ�����ж� AD �� OC ��λ�ù�ϵ����˵�����ɣ�
��3��̽������ a Ϊ���ٶ�ʱ����AOD �ǵ��������Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijѧУ��չ��������Ƽ����±������,��ϲ�����������������һ��ң�س���ֱ�߹��AC������ֱ���˶���ģ��.�ס�������ͬʱ�ֱ��A,B����,�ع������C��,��AC��,���ٶ����ҵ��ٶȵ�1.5��,��t�ֺ�ס�����ң�س���B���ľ���ֱ�Ϊd1,d2(��λ:��),��d1,d2��t�ĺ�����ϵ��ͼ,�Ը���ͼ������������.

��1��������ҵ��ٶ�v2=________��/��;
��2��д��d1��t�ĺ�������ʽ;
��3�����ס�����ң�س��ľ��볬��10��ʱ�źŲ�����������,��̽��ʲôʱ����ң�س����źŲ�����������?
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com