
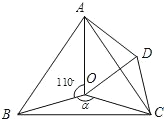
【题目】如图,点 O 是等边△ABC 内一点,∠AOB=110°,∠BOC=a.将△BOC 绕点 C 按顺时针方向旋转 60°得△ADC,则△ADC≌△BOC,连接 OD.
(1)求证:△COD 是等边三角形;
(2)当α=120°时,试判断 AD 与 OC 的位置关系,并说明理由;
(3)探究:当 a 为多少度时,△AOD 是等腰三角形?
【答案】(1)证明见解析;(2)证明见解析;(3)当 a 为 125°或 110°或 140°时,△AOD 是等腰三角形.
【解析】
(1)根据旋转得出CO=CD,∠DCO=60°,根据等边三角形的判定推出即可.
(2)求出∠ADO=∠COD=60°,根据平行线的判定推出即可.
(3)用∠α表示∠ADO、∠AOD、∠DAO,分为三种情况:①∠ADO=∠AOD,②∠ADO=∠OAD,③∠OAD=∠AOD,代入求出即可.
证明:(1)∵△ADC≌△BOC,
∴CO=CD,
∵将△BOC 绕点 C 按顺时针方向旋转 60°得△ADC,
∴∠DCO=60°,
∴△COD 是等边三角形.
(2)解:AD∥OC,
理由是:∵△DOC 是等边三角形,
∴∠CDO=∠DOC=60°,
∵∠α=120°,△COB≌△CDA,
∴∠ADC=∠COB=120°,
∴∠ADO=120°﹣60°=60°,
∴∠ADO=∠DOC=60°,
∴AD∥OC.
(3)解:∠AOD=360°﹣∠AOB﹣∠α﹣∠COD=360°﹣110°﹣∠α﹣60°=190°﹣∠α,∠ADO=∠ADC﹣∠CDO=∠α﹣60°,∠OAD=180°﹣∠AOD﹣∠ADO=180°﹣(∠α﹣60°)﹣(190°﹣∠α)=50°, 若∠ADO=∠AOD,即∠α﹣60°=190°﹣∠α,
解得:∠α=125°;
若∠ADO=∠OAD,则∠α﹣60°=50°, 解得:∠α=110°;
若∠OAD=∠AOD,即 50°=190°﹣∠α, 解得:∠α=140°;
即当 a 为 125°或 110°或 140°时,△AOD 是等腰三角形.


科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,AB=10,BC、CD、DA是⊙O的弦,且BC=CD=DA,若点P是直径AB上的一动点,则PD+PC的最小值为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
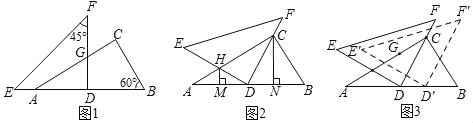
【题目】将一副三角尺按图1摆放,等腰直角三角尺的直角边DF恰好垂直平分AB,与AC相交于点G,![]() .
.
(1)求GC的长;
(2)如图2,将△DEF绕点D顺时针旋转,使直角边DF经过点C,另一直角边DE与AC相交于点H,分别过H、C作AB的垂线,垂足分别为M、N,通过观察,猜想MD与ND的数量关系,并验证你的猜想.
(3)在(2)的条件下,将△DEF沿DB方向平移得到△D′E′F′,当D′E′恰好经过(1)中的点G时,请直接写出DD′的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
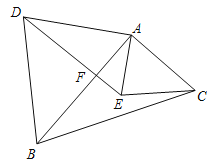
【题目】如图,在Rt△ABC和Rt△ADE中,∠BAC=∠DAE=90°,AB与DE相交于点F,连接DB、CE.
(1)若![]() ,求∠AFD的度数;
,求∠AFD的度数;
(2)若∠ADE=∠ABC,求证△ADB∽△AEC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,小明将一张长为4、宽为3的矩形纸片沿对角线剪开,得到两张三角形纸片(如图2),将这两张三角纸片摆成如图3的形状,但点B、C、F、D在同一条直线上,且点C与点F重合(在图3至图6中统一用点F表示).
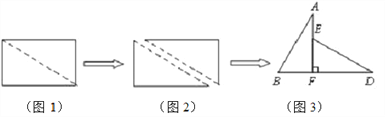
小明在对这两张三角形纸片进行如下操作时遇到了三个问题,请你帮助解决.
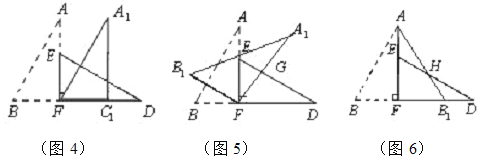
(1)将图3中的△ABF沿BD向右平移到图4中![]() 的位置,其中点B与点F 重合,请你求出平移的距离 ;
的位置,其中点B与点F 重合,请你求出平移的距离 ;
(2)在图5中若∠GFD=60°,则图3中的△ABF绕点 按 方向旋转 到图5的位置;
(3)将图3中的△ABF沿直线AF翻折到图6的位置,AB1交DE于点H,试问:△AEH和△HB1D的面积大小关系.说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
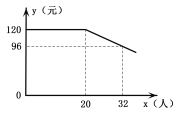
【题目】随着人们生活水平的提高,短途旅行日趋火爆.我市某旅行社推出“辽阳—葫芦岛海滨观光一日游”项目,团队人均报名费用y(元)与团队报名人数x(人)之间的函数关系如图所示,旅行社规定团队人均报名费用不能低于88元.旅行社收到的团队总报名费用为w(元).
(1)直接写出当x≥20时,y与x之间的函数关系式及自变量x的取值范围;
(2)儿童节当天旅行社收到某个团队的总报名费为3000元,报名旅游的人数是多少?
(3)当一个团队有多少人报名时,旅行社收到的总报名费最多?最多总报名费是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店购进一种商品,每件商品进价30元.试销中发现这种商品每天的销售量y(件)
与每件销售价x(元)的关系数据如下:
x | 30 | 32 | 34 | 36 |
y | 40 | 36 | 32 | 28 |
(1)已知y与x满足一次函数关系,根据上表,求出y与x之间的关系式(不写出自变量x的取值范围);
(2)如果商店销售这种商品,每天要获得150元利润,那么每件商品的销售价应定为多少元?
(3)设该商店每天销售这种商品所获利润为w(元),求出w与x之间的关系式,并求出每件商品销售价定为多少元时利润最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 与x轴最多有一个交点,现有以下三个结论:①该抛物线的对称轴在y轴左侧;②关于x的方程
与x轴最多有一个交点,现有以下三个结论:①该抛物线的对称轴在y轴左侧;②关于x的方程![]() 无实数根;③
无实数根;③![]() ≥0.其中,正确结论的个数为( )
≥0.其中,正确结论的个数为( )
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
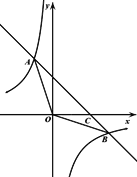
【题目】如图,一次函数y1=﹣x+2的图象与反比例函数![]() 的图象交于点A(﹣1,m),点B(n,﹣1).
的图象交于点A(﹣1,m),点B(n,﹣1).
(1)求反比例函数的解析式;
(2)当y1>y时,直接写出x的取值范围;
(3)求△AOB的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com