
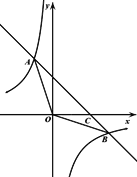
【题目】如图,一次函数y1=﹣x+2的图象与反比例函数![]() 的图象交于点A(﹣1,m),点B(n,﹣1).
的图象交于点A(﹣1,m),点B(n,﹣1).
(1)求反比例函数的解析式;
(2)当y1>y时,直接写出x的取值范围;
(3)求△AOB的面积.
【答案】(1)![]() ;(2)x<-1或0<x<3; (3)4.
;(2)x<-1或0<x<3; (3)4.
【解析】
(1)把A点坐标代入y1=﹣x+2可求出m=3,再把A(-1,3)代入![]() ,从而得到反比例函数解析式;
,从而得到反比例函数解析式;
(2)利用反比例函数解析式确定B点坐标,然后观察函数图象,写出一次函数图象在反比例函数图象上方所对应的自变量的取值范围即可;
(3)根据S△ABC=S△AOC+S△BOC求解即可.
(1)A(﹣1,m)代入y1=﹣x+2得m=1+2=3,∴A(-1,3),
将A点坐标(-1,3)代入![]() ,得
,得![]() ,解得,k=-3
,解得,k=-3

∴反比例函数的解析式为![]() ;
;
(2)易得,n=3,∴B(3,-1)
x<-1或0<x<3;
(3)如图,作AD成长x轴于点D,BE⊥x轴于点E,
则AD=3,BD=1,
易得,AB与x轴交点C(2,0),OC=2,
∴S△ABC=S△AOC+S△BOC=![]() .
.


科目:初中数学 来源: 题型:
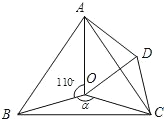
【题目】如图,点 O 是等边△ABC 内一点,∠AOB=110°,∠BOC=a.将△BOC 绕点 C 按顺时针方向旋转 60°得△ADC,则△ADC≌△BOC,连接 OD.
(1)求证:△COD 是等边三角形;
(2)当α=120°时,试判断 AD 与 OC 的位置关系,并说明理由;
(3)探究:当 a 为多少度时,△AOD 是等腰三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校开展“青少年科技创新比赛”活动,“喜洋洋”代表队设计了一个遥控车沿直线轨道AC做匀速直线运动的模型.甲、乙两车同时分别从A,B出发,沿轨道到达C处,在AC上,甲的速度是乙的速度的1.5倍,设t分后甲、乙两遥控车与B处的距离分别为d1,d2(单位:米),则d1,d2与t的函数关系如图,试根据图象解决下列问题.

(1)填空:乙的速度v2=________米/分;
(2)写出d1与t的函数表达式;
(3)若甲、乙两遥控车的距离超过10米时信号不会产生相互干扰,试探究什么时间两遥控车的信号不会产生相互干扰?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A在x轴上,OA=4,将线段OA绕点O顺时针旋转120°至OB的位置.
(1)求点B的坐标;
(2)求经过点A.O、B的抛物线的解析式;
(3)在此抛物线的对称轴上,是否存在点P,使得以点P、O、B为顶点的三角形是等腰三角形?若存在,求点P的坐标;若不存在,说明理由.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=ax2+bx+3 的图象与x轴分别交于A(1,0),B(3,0)两点,与y轴交于点C
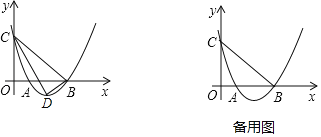
(1)求此二次函数解析式;
(2)点D为抛物线的顶点,试判断△BCD的形状,并说明理由;
(3)将直线BC向上平移t(t>0)个单位,平移后的直线与抛物线交于M,N两点(点M在y轴的右侧),当△AMN为直角三角形时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地上年度电价为0.8元/度,年用电量为1亿度,本年度计划将电价调至0.55~0.75元/度之间,经测算,若电价调至x元/度,则本年度新增用电量y(亿度)与(x-0.4)成反比例.又知当x=0.65时,y=0.8.
(1)求y与x之间的函数解析式;
(2)若每度电的成本价为0.3元,则电价调至多少时,本年度电力部门的收益将比上年度增加20%?[收益=用电量×(实际电价-成本价)]
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,直线y=﹣![]() x+a(a>0)分别与x 轴、y 轴交于A、B 两点,C、D 的坐标分别为 C(0,b)、D(2a,b﹣a)(b>a).
x+a(a>0)分别与x 轴、y 轴交于A、B 两点,C、D 的坐标分别为 C(0,b)、D(2a,b﹣a)(b>a).
(1)试判断四边形ABCD的形状,并说明理由;
(2)若点C、D关于直线AB的对称点分别为C′、D′.
①当b=3时,试问:是否存在满足条件的a,使得△BC′D′面积为![]() ?
?
②当点C′恰好落在x轴上时,试求a 与b的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
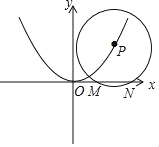
【题目】如图,⊙P的圆心P(m,n)在抛物线y=![]() 上.
上.
(1)写出m与n之间的关系式;
(2)当⊙P与两坐标轴都相切时,求出⊙P的半径;
(3)若⊙P的半径是8,且它在x轴上截得的弦MN,满足0≤MN≤2![]() 时,求出m、n的范围.
时,求出m、n的范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com