
【题目】如图,在![]() 中,
中,![]() 平分
平分![]() 交
交![]() 边于点
边于点![]() ,过点
,过点![]() 作
作![]() 交
交![]() 边于点
边于点![]() .且
.且![]() 平分
平分![]() ,若
,若![]() .
.

(1)求![]() 的度数.
的度数.
(2)求![]() 的长.
的长.
【答案】(1)30°;(2)4
【解析】
(1)根据角平分线的定义及平行线的性质可求得∠B=∠BCM=∠ACM,再根据∠ A=90°,即可求得∠B的度数;
(2)由(1)可求得∠AMN=∠B=30°,∠MCN=∠CMN ,进而可求得MN=2AN=4,MN=CN,即可解答.
(1)∵CM平分∠ACB,MN平分∠AMC,
∴∠ACM=∠BCM,∠AMN=∠CMN,
又∵MN∥BC,
∴∠AMN=∠B,∠CMN=∠BCM,
∴∠B=∠BCM=∠ACM,
∵∠A=90°,
∴∠B=![]() ×90°=30°;
×90°=30°;
(2)由(1)得,∠AMN=∠B=30°,∠MCN=∠CMN,∠A=90°,
∴MN=2AN=4,MN=CN,
∴CN=4.


科目:初中数学 来源: 题型:
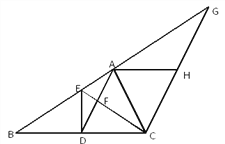
【题目】在△ABC中,D是BC的中点,且AD=AC,DE⊥BC,与AB相交于点E,EC与AD相交于点F.过C点作CG∥AD,交BA的延长线于G,过A作BC的平行线交CG于H点.
(1)若∠BAC=900,求证:四边形ADCH是菱形;
(2)求证:△ABC∽△FCD;
(3)若DE=3,BC=8,求△FCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋中装有2个红球(记为红1、红2),1个白球、1个黑球,这些球除颜色外都相同,将球搅匀.
(1)从中任意摸出1个球,恰好摸到红球的概率是 ;
(2)先从中任意摸出一个球,再从余下的3个球中任意摸出1个球,请用画树状图或列表法求两次都摸到红球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,M为BC上一点,F是AM的中点,EF⊥AM,垂足为F,交AD的延长线于点E,交DC于点N.
(1)求证:△ABM ∽△EFA;
(2)若AB=12,BM=5,求DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数y=kx+b的图象经过点A(﹣2,6),且与x轴相交于点B,与正比例函数y=3x的图象相交于点C,点C的横坐标为1.
(1)求k、b的值;
(2)若点D在y轴负半轴上,且满足S△COD=![]() S△BOC,求点D的坐标.
S△BOC,求点D的坐标.
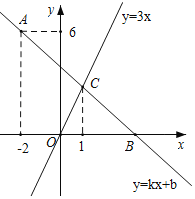
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】永辉超市进行有奖促销活动.活动规则:购买500元商品就可以获得一次转转盘的机会(转盘分为5个扇形区域,分别是特等奖、一等奖、二等奖、三等奖、不获奖),转盘指针停在哪个获奖区域就可以获得该区域相应等级奖品一件.商场工作人员在制作转盘时,将获奖扇形区域圆心角分配如下表:
奖次 | 特等奖 | 一等奖 | 二等奖 | 三等奖 |
圆心角 |
|
|
|
|
促销公告
凡购买我商场商品均有可能获得下列大奖:
特等奖:彩电一台 一等奖:自行车一辆 二等奖:圆珠笔一支 三等奖:卡通画一张
(1)获得圆珠笔的概率是多少?
(2)不获奖的概率是多少?
(3)如果不用转盘,请设计一种等效试验方案.(要求写清楚替代工具和实验规则)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A点坐标为(3,3),将△ABC 先向下平移4个单位得△A'B'C',再将△A'B'C'绕点O逆时针旋转180°得△A'B'C'.
(1)请你画出△A'B'C'和△A'B'C';
(2)点A'的坐标为 ;
(3)△ABC和△A'B'C'关于某个点中心对称,这个点的坐标为 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com