
ЗжЮі ЃЈ1ЃЉЯШНЋЗжФИгаРэЛЏЃЌдйНтЗНГЬМДПЩНтД№БОЬтЃЛ
ЃЈ2ЃЉИљОнМгМѕЯћдЊЗЈНтЗНГЬзщМДПЩНтД№БОЬтЃЎ
НтД№ НтЃКЃЈ1ЃЉ$\frac{\sqrt{2}}{\sqrt{2}-1}$x+$\frac{1}{\sqrt{2}+1}$=2x+1
ЗжФИгаРэЛЏЃЌЕУ
$\sqrt{2}ЃЈ\sqrt{2}+1ЃЉx+\sqrt{2}-1=2x-1$
ШЅРЈКХЃЌЕУ
$2x+\sqrt{2}x+\sqrt{2}-1=2x-1$
вЦЯюМАКЯВЂЭЌРрЯюЃЌЕУ
$\sqrt{2}x=-\sqrt{2}$
НтЕУЃЌx=-1ЃЛ
ЃЈ2ЃЉ$\left\{\begin{array}{l}{\sqrt{2}x-\sqrt{3}y=\sqrt{2}+\sqrt{3}}&{Ђй}\\{\sqrt{3}x-\sqrt{2}y=\sqrt{2}-\sqrt{3}}&{Ђк}\end{array}\right.$
$ЂйЁС\sqrt{2}-ЂкЁС\sqrt{3}$ЃЌЕУ
x=-5
НЋx=-5ДњШыЂйЃЌЕУ
y=-2$\sqrt{6}$-1
ЙЪдЗНГЬзщЕФНтЪЧ$\left\{\begin{array}{l}{x=-5}\\{y=-2\sqrt{6}-1}\end{array}\right.$ЃЎ
ЕуЦР БОЬтПМВщЖўДЮИљЪНЕФгІгУЃЌНтЬтЕФЙиМќЪЧУїШЗНтЗНГЬЕФЗНЗЈЃЌЛсЗжФИгаРэЛЏЃЎ


 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
 ШчЭМЃЌЦНааЫФБпаЮABCDЕФжмГЄЮЊ60РхУзЃЌBFЃЌDEЗжБ№ЮЊИпЃЌDCЕФГЄЮЊ18РхУзЃЎ
ШчЭМЃЌЦНааЫФБпаЮABCDЕФжмГЄЮЊ60РхУзЃЌBFЃЌDEЗжБ№ЮЊИпЃЌDCЕФГЄЮЊ18РхУзЃЎВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
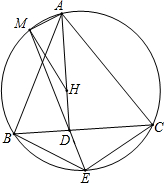 ШчЭМЃЌЁїABCЕФДЙаФЮЊHЃЌADЁЭBCгкDЃЌЕуEдкЁїABCЕФЭтНгдВЩЯЃЌЧвТњзу$\frac{BE}{CE}=\frac{AB}{AC}$ЃЌжБЯпEDНЛЭтНгдВгкЕуMЃЎЧѓжЄЃКЁЯAMH=90ЁуЃЎ
ШчЭМЃЌЁїABCЕФДЙаФЮЊHЃЌADЁЭBCгкDЃЌЕуEдкЁїABCЕФЭтНгдВЩЯЃЌЧвТњзу$\frac{BE}{CE}=\frac{AB}{AC}$ЃЌжБЯпEDНЛЭтНгдВгкЕуMЃЎЧѓжЄЃКЁЯAMH=90ЁуЃЎВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
| AЃЎ | -2ЃЌ-1ЃЌ0 | BЃЎ | 0ЃЌ1 | CЃЎ | -1ЃЌ0 | DЃЎ | ВЛДцдк |
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com