
分析 读题知(1)已知三个点的坐标,可以求出相应线段的长度,运用三角函数可以证明∠ACO=∠BAO,进一步证明∠BAC=90°;
(2)只需证明∠CDE=∠ABD,∠DCE=∠BAF,即可证明相似;
当四边形ABND为矩形时,根据直角三角形AOB和直角三角形ABN相似,可求AN长度,进一步求出OM,运用三角函数求解即可;
(3)根据点D在线段AC上,和线段AC的延长线上分别讨论求解.
解答 解:由点A(0,2),B(1,0),C(-4,0)可知:OA=2,OC=4,OB=1,
在直角三角形AOC和直角三角形AOB中,根据勾股定理可求:AC=$\sqrt{O{A}^{2}+O{C}^{2}}$=2$\sqrt{5}$,
AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=$\sqrt{5}$.
(1)在直角三角形AOC和直角三角形AOB中,tan∠ACO=$\frac{AO}{OC}$=$\frac{1}{2}$,tan∠BAO=$\frac{OB}{OA}$=$\frac{1}{2}$,所以∠ACO=∠BAO,
∵∠ACO+∠CAO=90°,
∴∠BAO+∠CAO=90°,∠BAC=90°,
∴△ABC是直角三角形.
(2)①由(1)知:∠BAC=90°,∴BD是圆M的直径,
∵DE是圆M的切线,∴∠BDE=90°.
∴∠CDE+∠ADB=90°,又∠ADB+∠ABD=90°,∴∠CDE=∠ABD,
∵∠DCE+∠ABO=90°,∠ABO+∠BAF=90°,∴∠DCE=∠BAF
∴△CDE∽△ABF.
②当四边形ABND为矩形时,∵∠ABN=90°,∴AN是圆的直径,由OB是直角三角形ABN的斜边上的高线,由∠BAO=∠BA0,∠BOA=∠ABN=90°,
∴△AOB∽△ABN,
∴$\frac{AB}{AN}$=$\frac{OA}{AB}$,
∴AB2=OA×AN,
∵OA=2,AB=$\sqrt{5}$,可求:AN=$\frac{5}{2}$,
∴ON=$\frac{1}{2}$,OM=MN-ON=$\frac{3}{4}$,
在直角三角形OBN中,
tan∠DBC=$\frac{OM}{OB}$=$\frac{3}{4}$.
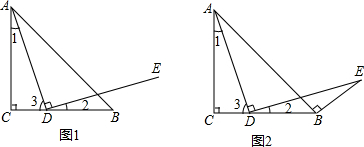
(3)若点D 在线段AC上,
如图2:由①知△CDE∽△ABF可得:$\frac{DE}{BF}=\frac{CD}{AB}=\frac{2}{3}$,AC=2$\sqrt{5}$,
由$\frac{CD}{CA}$=$\frac{1}{3}$,可得:CD=$\frac{2\sqrt{5}}{3}$,AD=$\frac{4\sqrt{5}}{3}$,
在直角三角形ABD中,由勾股定理可求:BD=$\sqrt{A{D}^{2}+A{B}^{2}}$=$\frac{5\sqrt{5}}{3}$,
∵∠CBD=∠FBO,∠BOF=∠BDE=90°,
∴△BFO∽△BED,
∴$\frac{OF}{ED}=\frac{OB}{BD}$,
设:DE=2x,则BF=3x,由勾股定理得:OF=$\sqrt{B{F}^{2}-O{B}^{2}}$=$\sqrt{(3x)^{2}-1}$,
∴$\frac{\sqrt{(3x)^{2}-1}}{2x}=\frac{1}{\frac{5\sqrt{5}}{3}}$,解得:x=$\frac{5\sqrt{5}}{33}$,
∴DE=$\frac{10\sqrt{5}}{33}$,BF=$\frac{5\sqrt{5}}{11}$,DF=BD-DF=$\frac{40\sqrt{5}}{33}$,
∴$\frac{DE}{DF}$=$\frac{1}{4}$,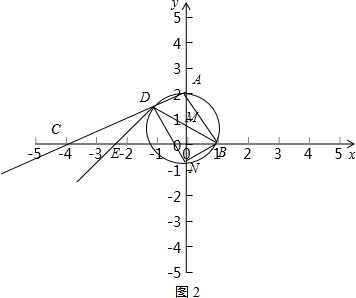
若点D在线段AC的延长线上,
如图3:∵DE是圆M的切线,
∴∠BDE=90°
∴∠EDC+∠CDB=90°
∵∠ABD+∠CDB=90°
∴∠EDC=∠ABD,
∵∠DEB+∠DBE=90°,∠DBE+∠OFB=90°
∴∠DEB=∠OFB,
∴△CDE∽△ABF,可得:$\frac{DE}{BF}=\frac{CD}{AB}=\frac{2}{3}$,AC=2$\sqrt{5}$,
由$\frac{CD}{CA}$=$\frac{1}{3}$,可得:CD=$\frac{2\sqrt{5}}{3}$,∴AD=AC+CD=$\frac{8\sqrt{5}}{3}$,
由勾股定理得:BD=$\sqrt{A{D}^{2}+A{B}^{2}}$=$\frac{\sqrt{365}}{3}$,
∵∠CBD=∠FBO,∠BOF=∠BDE=90°,
∴△BFO∽△BED,
∴$\frac{OF}{ED}=\frac{OB}{BD}$,
设:DE=2x,则BF=3x,
由勾股定理得:OF=$\sqrt{B{F}^{2}-O{B}^{2}}$=$\sqrt{(3x)^{2}-1}$,
∴$\frac{\sqrt{(3x)^{2}-1}}{2x}$=$\frac{1}{\frac{\sqrt{365}}{3}}$,
解得:x=$\frac{\sqrt{365}}{57}$,
∴DE=2x=$\frac{2\sqrt{365}}{57}$,BF=3x=$\frac{3\sqrt{365}}{57}$,DF=BD-DF=$\frac{16\sqrt{365}}{57}$,
∴$\frac{DE}{DF}$=$\frac{1}{8}$.
综上所述:$\frac{DE}{DF}$的值是$\frac{1}{4}$或$\frac{1}{8}$.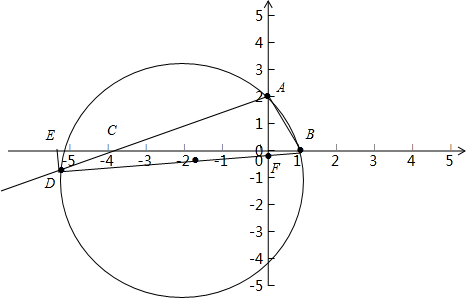
图3
点评 此题主要考察二次函数与圆的综合性问题,熟练应用勾股定理,相似的性质和判定,以及圆的相关性质是解题的关键.


科目:初中数学 来源: 题型:选择题
| A. | x2-x+1=0 | B. | $\sqrt{x-2}$=1-x | C. | $\frac{1-x}{{x}^{2}-x}$=0 | D. | $\frac{1-x}{{x}^{2}-x}$=1 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,为测量河两岸相对两电线杆A、B间的距离,在距A点16m的C处(AC⊥AB),测得∠ACB=52°,则A、B之间的距离应为( )
如图,为测量河两岸相对两电线杆A、B间的距离,在距A点16m的C处(AC⊥AB),测得∠ACB=52°,则A、B之间的距离应为( )| A. | 16sin52°m | B. | 16cos52°m | C. | 16tan52°m | D. | $\frac{16}{tan52°}$m |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
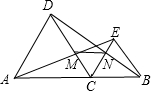 如图,点C是线段AB上的任意一点(C点不与A、B点重合),分别以AC、BC为边在直线AB的同侧作等边三角形△ACD和等边三角形BCE,AE与CD相交于点M,BD与CE相交于点N.
如图,点C是线段AB上的任意一点(C点不与A、B点重合),分别以AC、BC为边在直线AB的同侧作等边三角形△ACD和等边三角形BCE,AE与CD相交于点M,BD与CE相交于点N.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com