
【题目】如图,等边△ABC的边长是2,D、E分别为AB、AC的中点,延长BC至点F,使CF= ![]() BC,连结CD和EF.
BC,连结CD和EF.
(Ⅰ)求证:四边形CDEF是平行四边形;
(Ⅱ)求四边形BDEF的周长.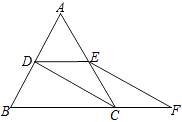
【答案】试题解析: (Ⅰ)∵D、E分别是AB,AC中点
∴DE∥BC,DE= ![]() BC
BC
∵CF= ![]() BC
BC
∴DE=CF
∴四边形CDEF是平行四边形
(Ⅱ) ∵四边形DEFC是平行四边形,
∴DC=EF,
∵D为AB的中点,等边△ABC的边长是2,
∴AD=BD=1,CD⊥AB,BC=2,
∴DC=EF= ![]()
∴四边形BDEF的周长为5+ ![]()
【解析】(Ⅰ)直接利用三角形中位线定理得出DE∥BC,再利用平行四边形的判定方法得出答案;(Ⅱ)分别计算BD、DE、EF、BF的长,再求四边形BDEF的周长即可.
【考点精析】认真审题,首先需要了解三角形中位线定理(连接三角形两边中点的线段叫做三角形的中位线;三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半).


科目:初中数学 来源: 题型:
【题目】如图,①②③④⑤五个平行四边形拼成一个含30度内角的菱形EFGH(不重叠无缝隙).若①②③④四个平行四边形面积的和为26cm2 , 四边形ABCD面积是19cm2 , 则①②③④四个平行四边形周长的总和为( )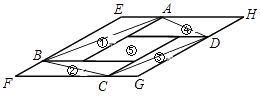
A.96cm
B.64cm
C.48cm
D.36cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们规定:将一个平面图形分成面积相等的两部分的直线叫做该平面图形的“等积线”,等积线被这个平面图形截得的线段叫做该图形的“等积线段”(例如三角形的中线就是三角形的等积线段).已知菱形的边长为4,且有一个内角为60°,设它的等积线段长为m,则m的取值范围是.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A的坐标为(-1,0),点B的坐标为(4,0),经过点A点B抛物线y=x+bx+c与y轴交于点C.
(1)求抛物线的关系式.
(2)△ABC的外接圆与y轴交于点D,在抛物线上是否存在点M使S△MBC=S△DBC,若存在,请求出点M的坐标.
(3)点P是直线y=-x上一个动点,连接PB,PC,当PB+PC+PO最小时,求点P的坐标及其最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列识别图形不正确的是( )
A.有一个角是直角的平行四边形是矩形
B.有三个角是直角的四边形是矩形
C.对角线相等的四边形是矩形
D.对角线互相平分且相等的四边形是矩形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有下列四个命题,其中正确的个数为( )
①两条对角线互相平分的四边形是平行四边形②两条对角线相等的四边形是菱形③两条对角线互相垂直的四边形是正方形④两条对角线相等且互相垂直的四边形是正方形
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】能判定一个四边形是菱形的条件是( )
A. 对角线互相平分且相等 B. 对角线互相垂直且相等
C. 对角线互相垂直且对角相等 D. 对角线互相垂直,且一条对角线平分一组对角
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com