练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】计算：
    （1）3a2b3÷ a3b ab3
    （2）（ ）3（ ）4÷（ ）3 ．

    【答案】
    （1）解：3a2b3÷（ a3b） ab3=（3× × ）a2﹣3+1b3﹣1+3= b5
    （2）解：原式=﹣ （﹣ ）=
    【解析】（1）根据单项式相乘相乘，把他们的系数，相同字母分别相乘，对于只在一个单项式里含有的字母，则连同它的指数作为积的一个因式．单项式除以单项式，把系数，同底数幂分别相除后，作为商的因式；对于只在被除式里含有的字母，则连同他的指数一起作为商的一个因式进行计算即可；（2）先把各个分式进行乘方运算，再进行分式的乘除运算，注意结果要化简．
    【考点精析】解答此题的关键在于理解单项式乘单项式的相关知识，掌握单项式与单项式相乘，把他们的系数，相同字母的幂分别相乘，其余字母连同他的指数不变，作为积的因式．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】下列分解因式正确的是

    A．－a＋a3=－a(1＋a2)B．2a－4b＋2=2(a－2b)

    C．a2－4=(a－2)2 D．a2－2a＋1=(a－1)2

    查看答案和解析>>

    科目：初中数学 来源： 题型：

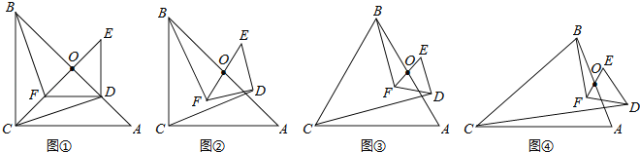
    【题目】如图①，△ABC与△DEF都是等腰直角三角形，∠ACB=∠EDF=90°，且点D在AB边上，AB、EF的中点均为O，连结BF、CD、CO，显然点C、F、O在同一条直线上，可以证明△BOF≌△COD，则BF=CD．

    解决问题

    （1）将图①中的Rt△DEF绕点O旋转得到图②，猜想此时线段BF与CD的数量关系，并证明你的结论；

    （2）如图③，若△ABC与△DEF都是等边三角形，AB、EF的中点均为O，上述（1）中的结论仍然成立吗？如果成立，请说明理由；如不成立，请求出BF与CD之间的数量关系；

    （3）如图④，若△ABC与△DEF都是等腰三角形，AB、EF的中点均为0，且顶角∠ACB=∠EDF=α，请直接写出的值（用含α的式子表示出来）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1所示，在A，B两地之间有汽车站C站，客车由A地驶往C站，货车由B地驶往A地．两车同时出发，匀速行驶．图2是客车、货车离C站的路程y1，y2（千米）与行驶时间x（小时）之间的函数关系图象．

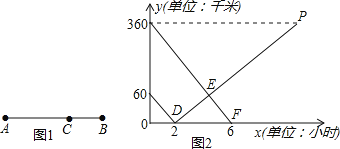
    （1）填空：A，B两地相距 千米；

    （2）求两小时后，货车离C站的路程y2与行驶时间x之间的函数关系式；

    （3）客、货两车何时相遇？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】解答题
    （1）一个数的绝对值是指在数轴上表示这个数的点到的距离；
    （2）若|a|=﹣a，则a0；
    （3）有理数a、b在数轴上的位置如图所示，请化简|a|+|b|+|a+b|．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，小红将一张直角梯形纸片沿虚线剪开，得到矩形和三角形两张纸片，测得AB=15，AD=12．在进行如下操作时遇到了下面的几个问题，请你帮助解决．

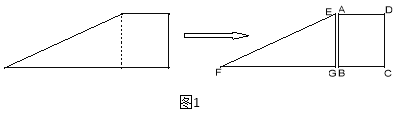
    （1）将△EFG的顶点G移到矩形的顶点B处，再将三角形绕点B顺时针旋转使E点落在CD边上，此时，EF恰好经过点A（如图2）求FB的长度

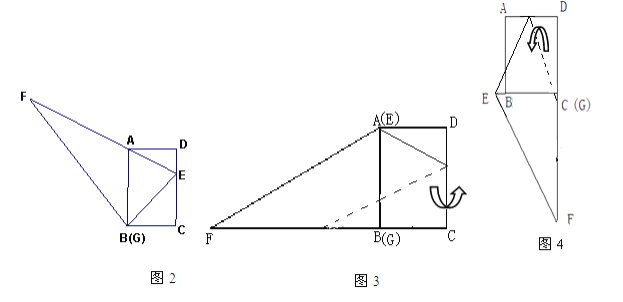
    （2）在（1）的条件下，小红想用△EFG包裹矩形ABCD,她想了两种包裹的方法如图3、图4，请问哪种包裹纸片的方法使得未包裹住的面积大？（纸片厚度忽略不计）请你通过计算说服小红。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知AM∥CN，点B为平面内一点，AB⊥BC于B．
    （1）如图1，直接写出∠A和∠C之间的数量关系；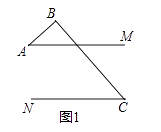

    （2）如图2，过点B作BD⊥AM于点D，求证：∠ABD=∠C；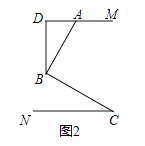

    （3）如图3，在（2）问的条件下，点E、F在DM上，连接BE、BF、CF，BF平分∠DBC，BE平分∠ABD，若∠FCB+∠NCF=180°，∠BFC=3∠DBE，求∠EBC的度数．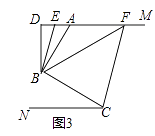

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，等边△ABC的边长是2，D、E分别为AB、AC的中点，延长BC至点F，使CF＝ BC，连结CD和EF.
    （Ⅰ）求证：四边形CDEF是平行四边形；
    （Ⅱ）求四边形BDEF的周长.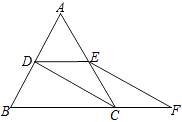

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】平面上A、B两点间的距离是指（ ）
    A.经过A，B两点的直线
    B.射线AB
    C.A，B两点间的线段
    D.A，B两点间线段长度

    查看答案和解析>>

    同步练习册答案