
【题目】已知AM∥CN,点B为平面内一点,AB⊥BC于B.
(1)如图1,直接写出∠A和∠C之间的数量关系; 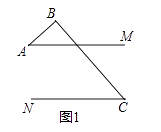
(2)如图2,过点B作BD⊥AM于点D,求证:∠ABD=∠C; 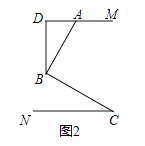
(3)如图3,在(2)问的条件下,点E、F在DM上,连接BE、BF、CF,BF平分∠DBC,BE平分∠ABD,若∠FCB+∠NCF=180°,∠BFC=3∠DBE,求∠EBC的度数. 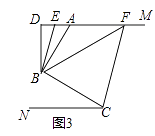
【答案】
(1)∠A+∠C=90°
(2)解:如图2,过点B作BG∥DM,
∵BD⊥AM,
∴DB⊥BG,即∠ABD+∠ABG=90°,
又∵AB⊥BC,
∴∠CBG+∠ABG=90°,
∴∠ABD=∠CBG,
∵AM∥CN,
∴∠C=∠CBG,
∴∠ABD=∠C

(3)解:如图3,过点B作BG∥DM,
∵BF平分∠DBC,BE平分∠ABD,
∴∠DBF=∠CBF,∠DBE=∠ABE,
由(2)可得∠ABD=∠CBG,
∴∠ABF=∠GBF,
设∠DBE=α,∠ABF=β,则
∠ABE=α,∠ABD=2α=∠CBG,∠GBF=β=∠AFB,∠BFC=3∠DBE=3α,
∴∠AFC=3α+β,
∵∠AFC+∠NCF=180°,∠FCB+∠NCF=180°,
∴∠FCB=∠AFC=3α+β,
△BCF中,由∠CBF+∠BFC+∠BCF=180°,可得
(2α+β)+3α+(3α+β)=180°,①
由AB⊥BC,可得
β+β+2α=90°,②
由①②联立方程组,解得α=15°,
∴∠ABE=15°,
∴∠EBC=∠ABE+∠ABC=15°+90°=105°

【解析】解:(1)如图1,∵AM∥CN,
∴∠C=∠AOB,
∵AB⊥BC,
∴∠A+∠AOB=90°,
∴∠A+∠C=90°,
故答案为:∠A+∠C=90°;
(1)根据平行线的性质以及直角三角形的性质进行证明即可;(2)先过点B作BG∥DM,根据同角的余角相等,得出∠ABD=∠CBG,再根据平行线的性质,得出∠C=∠CBG,即可得到∠ABD=∠C;(3)先过点B作BG∥DM,根据角平分线的定义,得出∠ABF=∠GBF,再设∠DBE=α,∠ABF=β,根据∠CBF+∠BFC+∠BCF=180°,可得(2α+β)+3α+(3α+β)=180°,根据AB⊥BC,可得β+β+2α=90°,最后解方程组即可得到∠ABE=15°,进而得出∠EBC=∠ABE+∠ABC=15°+90°=105°.


 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,AD平分∠BAC,DE⊥AB于E,DF⊥AC于F,则下列五个结论:①AD上任意一点到AB,AC两边的距离相等;②AD上任意一点到B,C两点的距离相等;③AD⊥BC,且BD=CD;④∠BDE=∠CDF;⑤AE=AF.其中,正确的有( ) 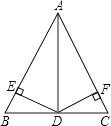
A.2个
B.3个
C.4个
D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图一根木棒放在数轴上,木棒的左端与数轴上的点A重合,右端与点B重合. ![]()
(1)若将木棒沿数轴向右水平移动,则当它的左端移动到B点时,它的右端在数轴上所对应的数为20;若将木棒沿数轴向左水平移动,则当它的右端移动到A点时,则它的左端在数轴上所对应的数为5(单位:cm),由此可得到木棒长为cm.
(2)由题(1)的启发,请你能借助“数轴”这个工具帮助小红解决下列问题:
问题:一天,小红去问曾当过数学老师现在退休在家的爷爷的年龄,爷爷说:“我若是你现在这么大,你还要40年才出生;你若是我现在这么大,我已经125岁,是老寿星了,哈哈!”,请求出爷爷现在多少岁了?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC,∠BAC=90°,分别过B,C向过点A的直线作垂线,垂足分别为点E,F.
(1)如图(1),过A的直线与斜边BC不相交时,求证:①△ABE≌△CAF; ②EF=BE+CF 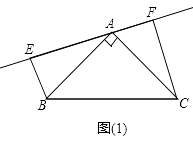
(2)如图(2),过A的直线与斜边BC相交时,其他条件不变,若BE=10,CF=3,试求EF的长. 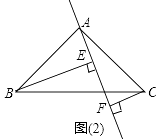
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,①②③④⑤五个平行四边形拼成一个含30度内角的菱形EFGH(不重叠无缝隙).若①②③④四个平行四边形面积的和为26cm2 , 四边形ABCD面积是19cm2 , 则①②③④四个平行四边形周长的总和为( )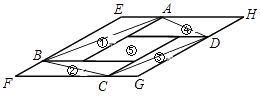
A.96cm
B.64cm
C.48cm
D.36cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们规定:将一个平面图形分成面积相等的两部分的直线叫做该平面图形的“等积线”,等积线被这个平面图形截得的线段叫做该图形的“等积线段”(例如三角形的中线就是三角形的等积线段).已知菱形的边长为4,且有一个内角为60°,设它的等积线段长为m,则m的取值范围是.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列识别图形不正确的是( )
A.有一个角是直角的平行四边形是矩形
B.有三个角是直角的四边形是矩形
C.对角线相等的四边形是矩形
D.对角线互相平分且相等的四边形是矩形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用一元一次方程解下列应用题
据国家统计局发布的数据显示,在我国的664个城市中,按水资源可分为暂不缺水城市、一般缺水城市和严重缺水城市三类.其中,暂不缺水城市比严重缺水城市的4倍少50个,一般缺水城市是严重缺水城市的2倍.
(1)求严重缺水城市有多少个?
(2)为了解决缺水的问题,国家启动了多个水利工程,缓解了部分严重缺水城市的情况,使一般性缺水城市的数目是严重缺水城市的9倍,求现在一般性缺水的城市有多少个?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com