
【题目】如图,已知△ABC中,AB=AC,∠BAC=90°,分别过B,C向过点A的直线作垂线,垂足分别为点E,F.
(1)如图(1),过A的直线与斜边BC不相交时,求证:①△ABE≌△CAF; ②EF=BE+CF 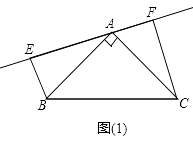
(2)如图(2),过A的直线与斜边BC相交时,其他条件不变,若BE=10,CF=3,试求EF的长. 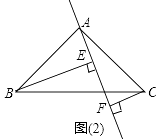
【答案】
(1)证明:
①∵BE⊥EF,CF⊥EF,
∴∠AEB=∠CFA=90°,
∴∠EAB+∠EBA=90°,
∵∠BAC=90°,
∴∠EAB+∠FAC=90°,
∴∠EBA=∠FAC,
在△AEB与△CFA中

∴△ABE≌△CAF(AAS),
②∵△ABE≌△CAF,
∴EA=FC,EB=FA,
∴EF=AF+AE
=BE+CF
(2)解:∵BE⊥AF,CF⊥AF
∴∠AEB=∠CFA=90°
∴∠EAB+∠EBA=90°
∵∠BAC=90°
∴∠EAB+∠FAC=90°
∴∠EBA=∠FAC,
在△AEB与△CFA中

∴△ABE≌△CAF(AAS),
∴EA=FC,EB=FA,
∴EF=FA﹣EA=EB﹣FC=10﹣3=7
【解析】(1)①由条件可求得∠EBA=FAC,利用AAS可证明△ABE≌△CAF;②利用全等三角形的性质可得EA=FC,EB=FA,利用线段的和差可证得结论;(2)同(1)可证明△ABE≌△CAF,可证得EF=FA﹣EA,代入可求得EF的长.


科目:初中数学 来源: 题型:
【题目】解答题
(1)一个数的绝对值是指在数轴上表示这个数的点到的距离;
(2)若|a|=﹣a,则a0;
(3)有理数a、b在数轴上的位置如图所示,请化简|a|+|b|+|a+b|. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
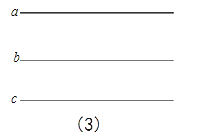
【题目】在正方形网格中以点A为圆心,AB为半径作圆A交网格于点C(如图(1)),过点C作圆的切线交网格于点D,以点A为圆心,AD为半径作圆交网格于点E(如图(2)).
问题:
(1)求∠ABC的度数;
(2)求证:△AEB≌△ADC;
(3)△AEB可以看作是由△ADC经过怎样的变换得到的?并判断△AED的形状(不用说明理由).
(4)如图(3),已知直线a,b,c,且a∥b,b∥c,在图中用直尺、三角板、圆规画等边三角形A′B′C′使三个顶点A′,B′,C′,分别在直线a,b,c上.要求写出简要的画图过程,不需要说明理由.
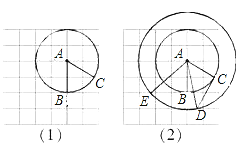
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AM∥CN,点B为平面内一点,AB⊥BC于B.
(1)如图1,直接写出∠A和∠C之间的数量关系; 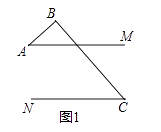
(2)如图2,过点B作BD⊥AM于点D,求证:∠ABD=∠C; 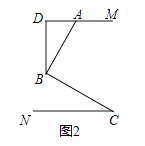
(3)如图3,在(2)问的条件下,点E、F在DM上,连接BE、BF、CF,BF平分∠DBC,BE平分∠ABD,若∠FCB+∠NCF=180°,∠BFC=3∠DBE,求∠EBC的度数. 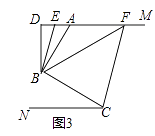
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用一个5倍的放大镜去观察一个三角形,对此,四位同学有如下说法:
甲说:三角形的每个内角都扩大到原来的5倍;
乙说:三角形的每条边都扩大到原来的5倍;
丙说:三角形的面积扩大到原来的5倍;
丁说:三角形的周长都扩大到原来的5倍.上述说法中正确的是( )
A. 甲和乙B. 乙和丙C. 丙和丁D. 乙和丁
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一家面临倒闭的企业在“调整产业结构,转变经营机制”的改革后,扭亏为盈. 下表是该企业2015年8~12月、2016年第一季度的月利润统计表:
根据以上信息,解答下列问题:
(1)2015年8月至2016年1月该企业利润的月平均利润为万元,月利润的中位数为万元;
(2)已知该企业2016年2、3月份的月利润的平均增长率相同,求这个平均增长率和2月份的月利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】科学实验证明,平面镜反射光线的规律是:射到平面镜上的光线和被反射出的光线与平面镜所夹的角相等.
(1)如图,一束光线m射到平面镜a上,被a反射到平面镜b上,又被b镜反射,若b反射出的光线n平行于m,且∠1=50°,则∠2= , ∠3=;
(2)在(1)中,若∠1=40°,则∠3= , 若∠1=55°,则∠3=;
(3)由(1)(2)请你猜想:当∠3=时,任何射到平面镜a上的光线m经过平面镜a和b的两次反射后,入射光线m与反射光线n总是平行的?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com