
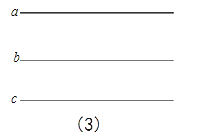
【题目】在正方形网格中以点A为圆心,AB为半径作圆A交网格于点C(如图(1)),过点C作圆的切线交网格于点D,以点A为圆心,AD为半径作圆交网格于点E(如图(2)).
问题:
(1)求∠ABC的度数;
(2)求证:△AEB≌△ADC;
(3)△AEB可以看作是由△ADC经过怎样的变换得到的?并判断△AED的形状(不用说明理由).
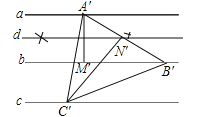
(4)如图(3),已知直线a,b,c,且a∥b,b∥c,在图中用直尺、三角板、圆规画等边三角形A′B′C′使三个顶点A′,B′,C′,分别在直线a,b,c上.要求写出简要的画图过程,不需要说明理由.
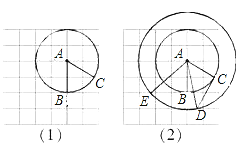
【答案】(1)∠ABC=60°;
(2)证明见解析;
(3)△AEB可以看作是由△ADC绕点A顺时针旋转60°得到的,△AED是等边三角形;
(4)作图及画图过程见解析.
【解析】试题分析:
(1)连接BC,通过证明△ABC是等边三角形,即可求出∠ABC的度数;
(2)在Rt△AEB与Rt△ADC中,通过HL证明△AEB≌△ADC;
(3)由旋转的性质即可得出△AED是等边三角形;
(4)利用HL定理可证△A′N′C′≌△A′M′B′,得∠C′A′N′=∠B′A′M′,于是∠B′A′C′=∠M′A′N′=60°,由A′B′=A′C′得△A′B′C′为等边三角形.
试题解析:
(1)连接BC,如图所示:
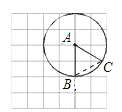
由网格可知点C在AB的中垂线上,
∴AC=BC,
∵AB=AC,∴AB=BC=AC,即△ABC是等边三角形.
∴∠ABC=60°;
(2)如图所示:
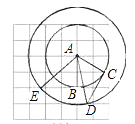
∵CD切⊙A于点C,
∴∠ACD=90°∠ABE=∠ACD=90°,
在Rt△AEB与Rt△ADC中,
∵AB=AC,AE=AD.
∴Rt△AEB≌Rt△ADC(HL);
(3)△AEB可以看作是由△ADC绕点A顺时针旋转60°得到的.△AED是等边三角形;
(4)①在直线a上任取一点,记为点A′,作A′M′⊥b,垂足为点M′;②作线段A′M′的垂直平分线,此直线记为直线d;③以点A′为圆心,A′M′长为半径画圆,与直线d交于点N′;④过点N′作N′C′⊥A′N′交直线c于点C′,连接A′C′;⑤以点A′为圆心,A′C′长为半径画圆,此圆交直线b于点B′;⑥连接A′B′、B′C′,则△A′B′C′为所求等边三角形.


科目:初中数学 来源: 题型:
【题目】已知|x﹣5|+(2y+6)2=0,A=﹣x2﹣2xy+y2 , B=﹣ ![]() x2﹣6xy+3y2 .
x2﹣6xy+3y2 .
(1)求y﹣x的值.
(2)求3A﹣[2A﹣B﹣4(A﹣B)]的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠A=α°,BO,CO分别是∠ABC,∠ACB的平分线,则∠BOC的度数是( ) 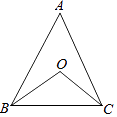
A.2α°
B.(α+60)°
C.(α+90)°
D.( ![]() α+90)°
α+90)°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC,∠BAC=90°,分别过B,C向过点A的直线作垂线,垂足分别为点E,F.
(1)如图(1),过A的直线与斜边BC不相交时,求证:①△ABE≌△CAF; ②EF=BE+CF 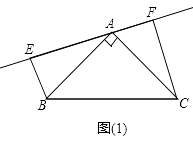
(2)如图(2),过A的直线与斜边BC相交时,其他条件不变,若BE=10,CF=3,试求EF的长. 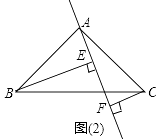
查看答案和解析>>
科目:初中数学 来源: 题型:
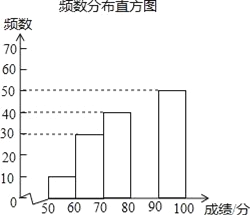
【题目】中华文明,源远流长;中华汉字,寓意深广,为了传承优秀传统文化,某校团委组织了一次全校3000名学生参加的“汉字听写”大赛,赛后发现所有参赛学生的成绩均不低于50分,为了更好地了解本次大赛的成绩分布情况,随机抽取了其中200名学生的成绩(成绩x取整数,总分100分)作为样本进行整理,得到下列不完整的统计图表:
成绩x/分 | 频数 | 频率 |
50≤x<60 | 10 | 0.05 |
60≤x<70 | 30 | 0.15 |
70≤x<80 | 40 | n |
80≤x<90 | m | 0.35 |
90≤x≤100 | 50 | 0.25 |
请根据所给信息,解答下列问题:
(1)m= ,n= ;
(2)请补全频数分布直方图;
(3)这次比赛成绩的中位数会落在 分数段;
(4)若成绩在90分以上(包括90分)的为“优”等,则该校参加这次比赛的3000名学生中成绩“优”等约有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com