
【题目】如图,△ABC中,∠A=α°,BO,CO分别是∠ABC,∠ACB的平分线,则∠BOC的度数是( ) 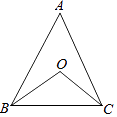
A.2α°
B.(α+60)°
C.(α+90)°
D.( ![]() α+90)°
α+90)°
【答案】D
【解析】解:∵∠A=α°,
∴∠ABC+∠ACB=180°﹣∠A=180°﹣α,
∵BO,CO分别是∠ABC,∠ACB的平分线,
∴∠OBC= ![]() ∠ABC,∠OCB=
∠ABC,∠OCB= ![]() ∠ACB,
∠ACB,
∴∠OBC+∠OCB= ![]() (∠ABC+∠ACB)=
(∠ABC+∠ACB)= ![]() ×(180°﹣α)=90°﹣
×(180°﹣α)=90°﹣ ![]() α,
α,
∴∠BOC=180°﹣(∠OBC+∠OCB)=180°﹣(90°﹣ ![]() α)=
α)= ![]() α+90°.
α+90°.
故选:D
【考点精析】掌握三角形的内角和外角是解答本题的根本,需要知道三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角.


科目:初中数学 来源: 题型:
【题目】盘锦市双台子区为了了解2016年初中毕业生毕业后的去向,对部分初三学生进行了抽样调查,就初三学生的四种去向:A.读普通高中;B.读职业高中C.直接进入社会就业;D.其它;进行数据统计,并绘制了两幅不完整的统计图(a)、(b).请问:
(1)该县共调查了______名初中毕业生;
(2)将两幅统计图中不完整的部分补充完整;
(3)若双台子区2016年初三毕业生共有4500人,请估计双台子区今年的初三毕业生中读普通高中的学生人数.
(4)老师想从甲、乙、丙、丁4位同学中随机选择两位同学了解他们毕业后的去向情况,请用树状图或列表法求选中甲同学的概率。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC是不规则三角形,若线段AD把△ABC分为面积相等的两部分,则线段AD应该是( )
A.三角形的角平分线
B.三角形的中线
C.三角形的高
D.以上都不对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形网格中以点A为圆心,AB为半径作圆A交网格于点C(如图(1)),过点C作圆的切线交网格于点D,以点A为圆心,AD为半径作圆交网格于点E(如图(2)).
问题:
(1)求∠ABC的度数;
(2)求证:△AEB≌△ADC;
(3)△AEB可以看作是由△ADC经过怎样的变换得到的?并判断△AED的形状(不用说明理由).
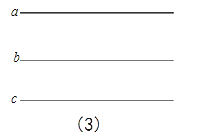
(4)如图(3),已知直线a,b,c,且a∥b,b∥c,在图中用直尺、三角板、圆规画等边三角形A′B′C′使三个顶点A′,B′,C′,分别在直线a,b,c上.要求写出简要的画图过程,不需要说明理由.
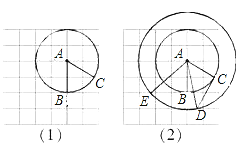
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某企业决定用![]() 万元援助灾区
万元援助灾区![]() 所学校,用于搭建帐篷和添置教学设备。根据各校不同的受灾情况,该企业捐款的分配方案如下:所有学校得到的捐款数都相等,到第
所学校,用于搭建帐篷和添置教学设备。根据各校不同的受灾情况,该企业捐款的分配方案如下:所有学校得到的捐款数都相等,到第![]() 所学校的捐款恰好分完,捐款的分配方法如下表所示. (其中
所学校的捐款恰好分完,捐款的分配方法如下表所示. (其中![]() ,
,![]() ,
,![]() 都是正整数)
都是正整数)
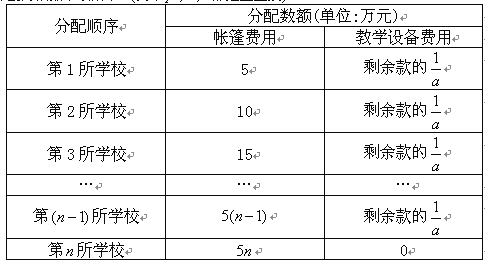
根据以上信息,解答下列问题:
(1)写出![]() 与
与![]() 的关系式;
的关系式;
(2)当![]() 时,该企业能援助多少所学校?
时,该企业能援助多少所学校?
(3)根据震区灾情,该企业计划再次提供不超过![]() 万元的捐款,按照原来的分配方案援助其它学校.若
万元的捐款,按照原来的分配方案援助其它学校.若![]() 由 (2)确定,则再次提供的捐款最多又可以援助多少所学校?
由 (2)确定,则再次提供的捐款最多又可以援助多少所学校?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E点为DF上的点,B为AC上的点,∠1=∠2,∠C=∠D.试说明:AC∥DF.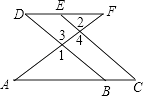
解:∵∠1=∠2(已知),
∠1=∠3(),
∴∠2=∠3(等量代换).
∴∥(同位角相等,两直线平行).
∴∠C=∠ABD ().
又∵∠C=∠D(已知),
∴∠D=∠ABD(等量代换).
∴AC∥DF().
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com