
【题目】如图,在矩形ABCD中,CD=2,AD=4,点P在BC上,将△ABP沿AP折叠,点B恰好落在对角线AC上的E点.O为AC上一点,⊙O经过点A,P.
(1)求证:BC是⊙O的切线;
(2)在边CB上截取CF=CE,点F是线段BC的黄金分割点吗?请说明理由.
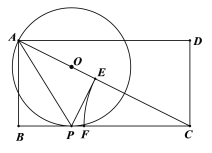
【答案】(1)见解析;(2)点F是线段BC的黄金分割点,理由见解析
【解析】
(1)因为是折叠,可得∠BAP=∠OAP,进而推导出AB∥OP,从而证垂直而得到切线;
(2)在Rt△ABC中,得出AC的长,在根据几何关系,可分别求出CF、BF的长度,得其比值为黄金比例
(1)证明:如图,连接OP,则OA=OP
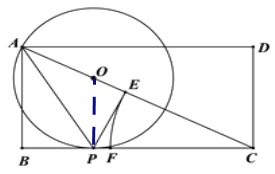
∴∠OAP=∠OPA.
由折叠知∠BAP=∠OAP,∴∠OPA=∠BAP. ∴AB∥OP.
又∵AB⊥BC,∴OP⊥BC.
∴BC是⊙O的切线.
(2)点F是线段BC的黄金分割点,理由如下:
在矩形ABCD中,∵AB=CD=2,BC=AD=4,
∴AC=![]()
又∵AE=AB=2,∴CE=CF=2![]() -2.
-2.
∴BF=BC-CF=6-2![]()
∵CF2=(2![]() -2)2=24-8
-2)2=24-8![]() ,
,
BFBC=4(6-2![]() )=24-8
)=24-8![]() ,
,
∴CF2=BFBC.
∴点F是线段BC的黄金分割点.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案科目:初中数学 来源: 题型:
【题目】如图1,为放置在水平桌面![]() 上的台灯,底座的高
上的台灯,底座的高![]() 为
为![]() .长度均为
.长度均为![]() 的连杆
的连杆![]() ,
,![]() 与
与![]() 始终在同一水平面上.
始终在同一水平面上.
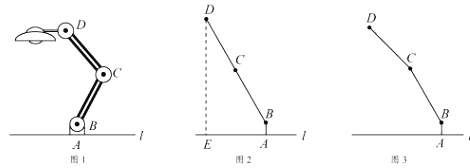
(1)旋转连杆![]() ,
,![]() ,使
,使![]() 成平角,
成平角,![]() ,如图2,求连杆端点
,如图2,求连杆端点![]() 离桌面
离桌面![]() 的高度
的高度![]() .
.
(2)将(1)中的连杆![]() 绕点
绕点![]() 逆时针旋转,使
逆时针旋转,使![]() ,如图3,问此时连杆端点
,如图3,问此时连杆端点![]() 离桌面
离桌面![]() 的高度是增加了还是减少?增加或减少了多少?(精确到
的高度是增加了还是减少?增加或减少了多少?(精确到![]() ,参考数据:
,参考数据:![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
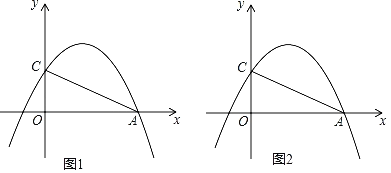
【题目】如图,在平面直角坐标系xOy中,二次函数y=﹣![]() x2+bx+c的图象经过点A(4,0),C(0,2).
x2+bx+c的图象经过点A(4,0),C(0,2).
(1)求抛物线的表达式;
(2)如图1,点E是第一象限的抛物线上的一个动点.当△ACE面积最大时,请求出点E的坐标;
(3)如图2,在抛物线上是否存在一点P,使∠CAP=45°?若存在,求点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,点G是等边三角形AOB的外心,点A在第一象限,点B坐标为(4,0),连结OG.抛物线y=ax(x﹣2)+1+![]() 的顶点为P.
的顶点为P.
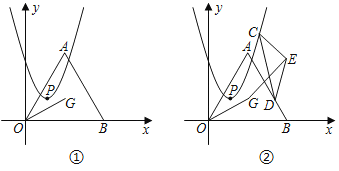
(1)直接写出点A的坐标与抛物线的对称轴;
(2)连结OP,求当∠AOG=2∠AOP时a的值.
(3)如图②,若抛物线开口向上,点C,D分别为抛物线和线段AB上的动点,以CD为底边构造顶角为120°的等腰三角形CDE(点C,D,E成逆时针顺序),连结GE.
①点Q在x轴上,当四边形GDQO为平行四边形时,求GQ的值;
②当GE的最小值为1时,求抛物线的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠A=90°,点D,E分别在AC,BC上,且CD·BC=AC·CE,以E为圆心,DE长为半径作圆,⊙E经过点B,与AB,BC分别交于点F,G.
(1)求证:AC是⊙E的切线;
(2)若AF=4,CG=5,
①求⊙E的半径;
②若Rt△ABC的内切圆圆心为I,则IE= .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“端午节”是我国的传统佳节,民间历来有吃“粽子”的习俗.我市某食品厂为了解市民对去年销量较好的肉馅粽、豆沙馅粽、红枣馅粽、蛋黄馅粽(以下分别用A,B,C,D表示)这四种不同口味粽子的喜爱情况,在节前对某居民区市民进行了抽样调查,并将调查情况绘制成如下两幅统计图(尚不完整).

请根据以上信息回答:
(1)将两幅不完整的图补充完整;
(2)本次参加抽样调查的居民有多少人?
(3)若居民区有8000人,请估计爱吃D粽的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
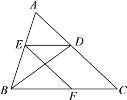
【题目】已知:如图,BD是△ABC的角平分线,点E、F分别在AB、BC上,且ED//BC,EF//AC.
(1)求证:BE=DE;
(2)当AB=AC时,试说明四边形EFCD为菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
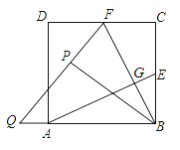
【题目】如图,在正方形ABCD中,E、F分别为BC、CD的中点,连接AE,BF交于点G,将△BCF沿BF对折,得到△BPF,延长FP交BA延长线于点Q,下列结论正确的个数是( )
①AE=BF;②AE⊥BF;③sin∠BQP=![]() ;④S四边形ECFG=2S△BGE.
;④S四边形ECFG=2S△BGE.
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中华文化,源远流长,在文学方面,《西游记》、《三国演义》、《水浒传》、《红楼梦》是我国古代长篇小说中的典型代表,被称为“四大古典名著”,某中学为了了解学生对四大古典名著的阅读情况,就“四大古典名著你读完了几部”的问题做法全校学生中进行了抽样调查,根据调查结果绘制城如图所示的两个不完整的统计图,请结合图中信息解决下列问题:
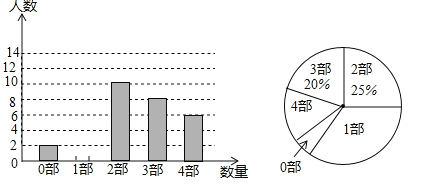
(1)本次调查所得数据的众数是 部,中位数是 部,扇形统计图中“1部”所在扇形的圆心角为 度.
(2)请将条形统计图补充完整;
(3)没有读过四大古典名著的两名学生准备从四大固定名著中各自随机选择一部来阅读,则他们选中同一名著的概率为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com