
【题目】在平面直角坐标系中,将一块等腰直角三角板ABC放在第一象限,斜靠在两条坐标轴上,∠ACB=900 , 且A(0,4),点C(2,0),BE⊥x轴于点E,一次函数y=x+b经过点B,交y轴于点D。
(1)求证;△AOC≌△CEB
(2)求△ABD的面积。
【答案】
(1)证明:∵△ABC是等腰直角三角形
∴∠ACB=900 , AC=BC
∴∠ACO+∠BCE=900
BE⊥CE,∴∠BCE+∠CBE=900
∴∠ACO=∠CBE
∴△AOC≌△CEB
(2)解:∵△AOC≌△CEB
∴BE=OC=2,CE=OA=4
∴点B的坐标为(6,2)
又一次函数y=x+b经过点B(6,2)
∴2=6+b
∴b=-4
∴点D的坐标为(0,-4)
∴ ![]()
在△ABD中,AD边上高的长度就是B点纵坐标的绝对值.
∴S△ABD= ![]() ×8×6=24
×8×6=24
∴△ABD的面积为24
【解析】(1)由等腰直角三角形的性质可证得AC=BC,∠ACO=∠CBE,进而可证得△AOC≌△CEB;(2)由(1)的全等,可得B坐标,代入解析式,可求出b,进而求出D坐标,AD的长,AD边上高的长度就是B点纵坐标,进而求出面积.


 黄冈创优卷系列答案
黄冈创优卷系列答案科目:初中数学 来源: 题型:
【题目】下列命题中:①有公共顶点且相等的角是对顶角;②直线外一点到这条直线的垂线段,叫做点到直线的距离;③互为邻补角的两个角的平分线互相垂直;④经过一点有且只有一条直线与已知直线平行.其中真命题的个数有( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 的图象过点C(0,1),顶点为Q(2,3),点D在x轴正半轴上,线段OD=OC.
的图象过点C(0,1),顶点为Q(2,3),点D在x轴正半轴上,线段OD=OC.
(1)求抛物线的解析式;
(2)抛物线上是否存在点M,使得⊿CDM是以CD为直角边的直角三角形?若存在,请求出M点的坐标;若不存在,请说明理由.
(3)将直线CD绕点C逆时针方向旋转45°所得直线与抛物线相交于另一点E,,连接QE.若点P是线段QE上的动点,点F是线段OD上的动点,问:在P点和F点的移动过程中,△PCF的周长是否存在最小值?若存在,求出这个最小值,若不存在,请说明理由。


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A,B的坐标分别为(1,0),(0,2),若将线段AB平移到A1B1,点A1,B1的坐标分别为(2,a),(b,3),则a22b的值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
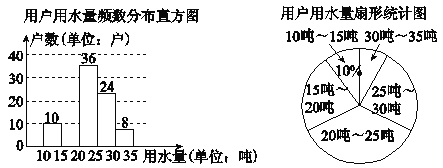
【题目】某市为提倡节约用水,准备实行自来水“阶梯计费”方式,用户用水不超出基本用水量的部分享受基本价格,超出基本用水量的部分实行超价收费,为更好地决策,自来水公司随机抽取了部分用户的用水量数据,并绘制了如图不完整的统计图(每组数据包括右端点但不包括左端点),请你根据统计图解答下列问题:
(1)此次抽样调查的样本容量是________;
(2)补全频数分布直方图,求扇形图中“15吨~20吨”部分的圆心角的度数;
(3)如果自来水公司将基本用水量定为每户25吨,那么该地区6万用户中约有多少用户的用水全部享受基本价格?
查看答案和解析>>
科目:初中数学 来源: 题型:
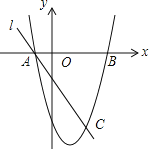
【题目】(本题满分12分)如图,抛物线y=x2﹣2x﹣3与x轴交于A、B两点(A点在B点左侧),直线l与抛物线交于A、C两点,其中C点的横坐标为2.
(1)求A、B、C三点的坐标;
(2)在抛物线的对称轴上找到点P,使得△PBC的周长最小,并求出点P的坐标;
(3)点G抛物线上的动点,在x轴上是否存在点F,使A、C、F、G为顶点四边形是平行四边形?如果存在,请直接写出F点坐标;如果不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com