
分析 根据题目给出的过程即可求出答案.
解答 解:(1)原式=$\frac{\sqrt{3}-\sqrt{2}}{(\sqrt{3}+\sqrt{2})(\sqrt{3}-\sqrt{2})}$=$\frac{\sqrt{3}-\sqrt{2}}{3-2}=\sqrt{3}-\sqrt{2}$;
(2)原式=$\frac{(\sqrt{n+1}-\sqrt{n})}{(\sqrt{n+1}+\sqrt{n})(\sqrt{n+1}-\sqrt{n})}$=$\sqrt{n+1}-\sqrt{n}$;
故答案为:$\sqrt{n+1}-\sqrt{n}$
(3)由(2)可知:
原式=$\sqrt{2}$-1+$\sqrt{3}-\sqrt{2}$+$\sqrt{4}$-$\sqrt{3}$+…+$\sqrt{100}$-$\sqrt{99}$
=-1+$\sqrt{100}$
=9
点评 本题考查二次根式的混合运算,涉及平方差公式,属于基础题型.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:解答题
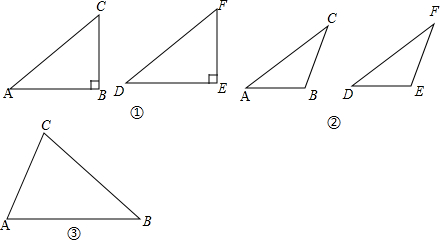
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
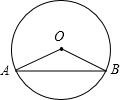 (1)如图,弦AB把⊙O分成2:7,∠AOB=80°;
(1)如图,弦AB把⊙O分成2:7,∠AOB=80°;查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com