
 如图,已知点E,F,G,H分别是正方形ABCD四条边上的点,并且AE=BF=CG=DH.求证:四边形EFGH是正方形.
如图,已知点E,F,G,H分别是正方形ABCD四条边上的点,并且AE=BF=CG=DH.求证:四边形EFGH是正方形. 分析 可通过证明△AEH,△DHG,△CGF,△BFE全等,先得出四边形EFGH是菱形,再证明四边形EFGH中一个内角为90°,从而得出四边形EFGH是正方形的结论
解答 解:四边形EFGH是正方形.
证明:∵AE=BF=CG=GH,
∴AH=DG=CF=BE.
∵∠A=∠B=∠C=∠D=90°,
∴△AEH≌△DHG≌△CGF≌△BFE,
∴EF=EH=HG=GF,∠EHA=∠HGD.
∴四边形EFGH是菱形.
∵∠EHA=∠HGD,∠HGD+∠GHD=90°,
∴∠EHA+∠GHD=90°.
∴∠EHG=90°.
∴四边形EFGH是正方形.
点评 本题主要考查了全等三角形的判定及性质、菱形的判定和性质、正方形的性质和判定,熟练掌握应用全等三角形的性质是解题的关键.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案科目:初中数学 来源: 题型:解答题
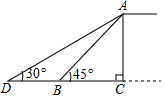 某市为缓解城市交通压力,决定修建人行天桥.原设计天桥的楼梯长AB=6m,∠ABC=45°,后考虑到安全因素,将楼梯脚B移到CB延长线上点D处,使∠ADC=30°.求BD的长.(结果保留根号).
某市为缓解城市交通压力,决定修建人行天桥.原设计天桥的楼梯长AB=6m,∠ABC=45°,后考虑到安全因素,将楼梯脚B移到CB延长线上点D处,使∠ADC=30°.求BD的长.(结果保留根号).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 碟子的个数 | 1 | 2 | 3 | 4 | … |
| 碟子的高度(单位:cm) | 2 | 2+1.5 | 2+3 | 2+4.5 | … |
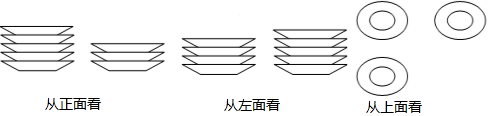
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com