练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
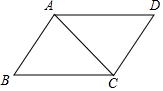
    8．如图，已知AB∥CD，AD∥CB，则△ABC≌△CDA的依据是（　　）
    A．SASB．ASAC．AASD．SSS

    分析 先根据平行线的性质得∠BAC=∠DCA，∠DAC=∠BCA，再加上公共边，则可利用“ASA”判断△ABC≌△CDA．

    解答 解：∵AB∥DC，AD∥BC，
    ∴∠BAC=∠DCA，∠DAC=∠BCA，
    而AC=CA，
    ∴△ABC≌△CDA（ASA）．
    故选B．

    点评 本题考查了全等三角形的判定：全等三角形的5种判定方法中，选用哪一种方法，取决于题目中的已知条件，若已知两边对应相等，则找它们的夹角或第三边；若已知两角对应相等，则必须再找一组对边对应相等，且要是两角的夹边，若已知一边一角，则找另一组角，或找这个角的另一组对应邻边．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    18．已知二次函数y=ax2+bx+c的图象经过点（-1，0）、（5，0）、（0、-5）．
    （1）求此二次函数的解析式；    
    （2）当0≤x≤5时，求此函数的最小值与最大值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

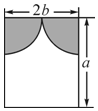    19．长方形窗户上的装饰物如图所示，它是由半径均为b的两个四分之一圆组成，则能射进阳光部分的面积是（　　）
    A．2a2-πb2B．2a2-$\frac{π}{2}$b2C．2ab-πb2D．2ab-$\frac{π}{2}$b2

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．计算：
    （1）2（3a-2b）-3（a-3b）
    （2）2xy2+2（3xy2-x2y）-2（xy2-x2y）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．如图，点A从原点出发沿数轴向左运动，同时，点B也从原点出发沿数轴向右运动，5秒后，两点相距15个单位长度．已知点B的速度是点A的速度的2倍（速度单位：单位长度/秒）．
    （1）求出点A、点B运动的速度，并在数轴上标出A、B两点从原点出发运动5秒时的位置；

    （2）若A、B两点从（1）中的位置开始，仍以原来的速度同时沿数轴向左运动，再过几秒时，原点恰好处在点A、点B的正中间？
    （3）若A、B两点从（1）中的位置开始，仍以原来的速度同时沿数轴向左运动时，另一点C同时从原点O位置出发向B点运动，且C的速度是点A的速度的一半；当C运动几秒后，C为AB的中点？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．已知关于x、y的多项式mx2+4xy-x-3x2+2nxy-4y合并后不含有二次项，求n-m的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

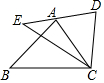    20．如图所示，△ABC≌△DEC，∠ACB=60°，∠BCD=100°，点A恰好落在线段ED上，则∠B的度数为（　　）
    A．50°B．60°C．55°D．65°

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．先化简（$\frac{{a}^{2}}{a+2}$-a+2）÷$\frac{4a}{{a}^{2}-4}$，再从-2，2，4，0中选择一个合适的数代入求值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    18．先化简，再求值：
    2（x3-2y2）-（x-2y）-（x-3y2+2x3），其中x=-2，y=-3．

    查看答案和解析>>

    同步练习册答案