
【题目】中秋节期间某水库养殖场为适应市场需求,连续用![]() 天时间,采用每天降低水位以减少捕捞成本的办法.对水库中某种鲜鱼进行捕捞销售,第
天时间,采用每天降低水位以减少捕捞成本的办法.对水库中某种鲜鱼进行捕捞销售,第![]() 天(
天(![]() 且
且![]() 为整数)的捕捞与销售的相关信息如下:
为整数)的捕捞与销售的相关信息如下:
鲜鱼销售单价(元 |
|
单位捕捞成本(元 |
|
捕捞量 |
|
假定该养殖场每天捕捞和销售的鲜鱼没有损失,且能在当天全部售出.
(1)求第![]() 天的收入
天的收入![]() (元)与
(元)与![]() (天)之间的函数关系式?(当天收入
(天)之间的函数关系式?(当天收入![]() 日销售额-日捕捞成本)
日销售额-日捕捞成本)
(2)在第几天![]() 取得最大值,最大值是多少?
取得最大值,最大值是多少?
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,![]() 和
和![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 在
在![]() 边上.
边上.
(1)如图1,连接![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的长度;
的长度;
(2)如图2,将![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() ,旋转过程中,直线
,旋转过程中,直线![]() 分别与直线
分别与直线![]() 交于点
交于点![]() ,当
,当![]() 是等腰三角形时,直接写出
是等腰三角形时,直接写出![]() 的值;
的值;
(3)如图3,将![]() 绕点
绕点![]() 顺时针旋转,使得点
顺时针旋转,使得点![]() 在同一条直线上,点
在同一条直线上,点![]() 为
为![]() 的中点,连接
的中点,连接![]() .猜想
.猜想![]() 和
和![]() 之间的数量关系并证明.
之间的数量关系并证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
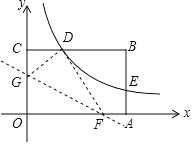
【题目】如图,矩形OABC的顶点A、C分别在x、y轴的正半轴上,点D为BC边上的点,AB=BD,反比例函数![]() 在第一象限内的图象经过点D(m,2)和AB边上的点E(n,
在第一象限内的图象经过点D(m,2)和AB边上的点E(n,![]() ).
).
(1)求m、n的值和反比例函数的表达式.
(2)将矩形OABC的一角折叠,使点O与点D重合,折痕分别与x轴,y轴正半轴交于点F,G,求线段FG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某企业设计了一款工艺品,每件的成本是50元,为了合理定价,投放市场进行试销.据市场调查,销售单价是100元时,每天的销售量是50件,而销售单价每降低1元,每天就可多售出5件,但要求销售单价不得低于成本
(1)求每天的销售利润y(元)与销售单价x(元)之间的函数关系式;
(2)求出销售单价为多少元时,每天的销售利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
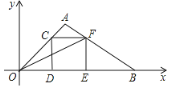
【题目】如图,点A 坐标为(1,1),点C是线段OA上的一个动点(不运动至O,A两点)过点C作CD⊥x轴,垂足为D,以CD为边在右侧作正方形CDEF,连接AF并延长交x轴的正半轴于点B,连接OF,若以B、E、F为顶点的三角形与△OEF相似,,则B的坐标是 ___________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD=BC,点E、F、G、H分别是AB、BD、CD、AC的中点,则四边形EFGH是( )
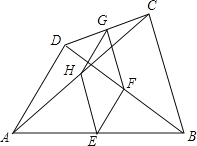
A.矩形B.菱形C.正方形D.平行四边形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com