
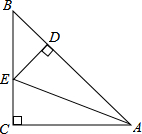
 如图,Rt△ABC,BC=AC,∠C=90°,AE平分∠BAC,且ED⊥AB于D,求证:EC=BD.
如图,Rt△ABC,BC=AC,∠C=90°,AE平分∠BAC,且ED⊥AB于D,求证:EC=BD.

 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
 已知:如图,函数y1=ax的图象与函数y2=
已知:如图,函数y1=ax的图象与函数y2=| k |
| x |
| k |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:
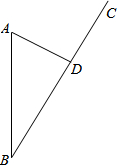 今年第九号台风“苏拉”登陆浙江,A市接到台风警报时,台风中心位于A市正南方向85km的B处,正以14km/h的速度沿BC方向移动.已知A市到BC的距离AD=40km,那么台风中心从B点移到D点经过多长时间?(计算结果精确到0.1小时)
今年第九号台风“苏拉”登陆浙江,A市接到台风警报时,台风中心位于A市正南方向85km的B处,正以14km/h的速度沿BC方向移动.已知A市到BC的距离AD=40km,那么台风中心从B点移到D点经过多长时间?(计算结果精确到0.1小时)查看答案和解析>>
科目:初中数学 来源: 题型:
| 20 |
| 7 |
| 3 |
| 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com